Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2
a) \(x^4-24x^2-25=0\) ( 1 )
Đặt \(t=x^2\) ( điều kiện \(t\ge0\) )
\(pt\left(1\right)\Leftrightarrow t^2-24t-25=0\)
\(\Delta=b^2-4ac\)
\(\Delta=676\)
\(\Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{24+\sqrt{676}}{2}=25\left(nhận\right)\\t_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{24-\sqrt{676}}{2}=-1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x^2=25\)
\(\Rightarrow x=\pm5\)
b)
\(\left\{{}\begin{matrix}2x-y=2\\9x+8y=34\end{matrix}\right.\)
Xét \(2x-y=2\)
\(\Rightarrow x=\dfrac{2+y}{2}\)
Ta có \(9x+8y=34\)
\(\Leftrightarrow\dfrac{9\left(2+y\right)}{2}+8y=34\)
\(\Leftrightarrow\dfrac{18+9y}{2}+8y=34\)
\(\Leftrightarrow\dfrac{18+25y}{2}=34\)
\(\Leftrightarrow18+25y=68\)
\(\Rightarrow y=2\)
\(\Rightarrow x=\dfrac{y+2}{2}=2\)
Vậy \(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Bài 3
a) \(x^2-5x+m-2=0\)
Thay \(m=-4\) vào phương trình
\(\Rightarrow x^2-5x-6=0\)
\(\Delta=b^2-4ac\)
\(\Delta=49\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{49}}{2}=6\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{49}}{2}=-1\end{matrix}\right.\)
b )
\(x^2-5x+m-2=0\)
\(\Delta=b^2-4ac\)
\(\Delta=33-4m\)
Theo định lý Viet
\(\Rightarrow\left\{{}\begin{matrix}P=x_1+x_2=\dfrac{-b}{a}\\S=x_1x_2=\dfrac{c}{a}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}P=x_1+x_2=5\\S=x_1x_2=m-2\end{matrix}\right.\)
Để phương trình có 2 nghiệm dương phân biệt
\(\Rightarrow\left\{{}\begin{matrix}\Delta>0\\P>0\\S>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}33-4m>0\\m-2>0\\5>0\left(đúng\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{33}{4}\\m>2\end{matrix}\right.\)
\(\Rightarrow2< m< \dfrac{33}{4}\)
Ta có \(2\left(\dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}}\right)=3\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}}=\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x_1}+\sqrt{x_2}}{\sqrt{x_1x_2}}=\dfrac{3}{2}\)
\(\Leftrightarrow\left(\dfrac{\sqrt{x_1}+\sqrt{x_2}}{\sqrt{x_1x_2}}\right)^2=\dfrac{9}{4}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x_1}+\sqrt{x_2}\right)^2}{x_1x_2}=\dfrac{9}{4}\)
\(\Leftrightarrow\dfrac{x_1+x_2+2\sqrt{x_1x_2}}{x_1x_2}=\dfrac{9}{4}\)
\(\Leftrightarrow\dfrac{5+\sqrt{m-2}}{m-2}=\dfrac{9}{4}\)
\(\Leftrightarrow20+4\sqrt{m-2}=9m-18\)
\(\Leftrightarrow4\sqrt{m-2}=9m-38\)
\(\Leftrightarrow64m-128=\left(9m-38\right)^2\)
\(\Leftrightarrow64m-128=81m^2-684m+1444\)
\(\Leftrightarrow81m^2-748m+1572=0\)
\(\Delta=b^2-4ac\)
\(\Delta=50176\)
\(\Rightarrow\left\{{}\begin{matrix}m_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{748+\sqrt{50176}}{162}=6\\m_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{748-\sqrt{50176}}{162}=\dfrac{262}{81}\end{matrix}\right.\)
Vì \(2< m< \dfrac{33}{4}\)
\(\Rightarrow m\in\left\{6;\dfrac{262}{81}\right\}\)

B D C E A Q H
1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến
=> D là trung điểm của BC. Theo trên ta có góc BEC = 900.
Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.
4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).
Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)
Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3
Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.
Vậy DE là tiếp tuyến của đường tròn (O) tại E.
5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED2 = OD2 – OE2 ↔ ED2 = 52 – 32 ↔ ED = 4cm

1. Định lí Pytago
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
ΔABC vuông tại A thì ta có:
AB2+AC2=BC2
a2+b2=c2

TRẢ LỜI:
Mệnh đề phủ định của P: P− “ π không là một số hữu tỉ”.
P là mệnh đề sai, P− là mệnh đề đúng.
Mệnh đề phủ định của Q: Q− “Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh thứ ba”.
Q là mệnh đề đúng, Q− là mệnh đề sai.
tk cho mk ha








 và
và  trên hình 5 cũng có độ dài bằng nhau, nhưng liệu chúng ta có nên nói rằng chúng bằng nhau và viết
trên hình 5 cũng có độ dài bằng nhau, nhưng liệu chúng ta có nên nói rằng chúng bằng nhau và viết  thì có nhận xét gì về độ dài và hướng của chúng?
thì có nhận xét gì về độ dài và hướng của chúng?
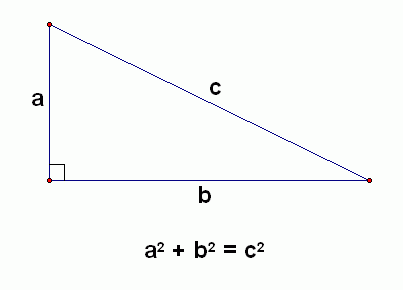
Câu 1.
a) ĐKXĐ: x ≥ 0, x ≠ 4.
Rút gọn:
b. x = 1/4 ∈ ĐKXĐ. Thay vào P, ta được:
Câu 2.
Gọi x, y (nghìn) lần lượt là giá của 1 quả dừa và 1 quả thanh long.
Điều kiện : 0 < x; y < 25.
Giải ra ta được : x = 20, y = 5 (thỏa mãn điều kiện bài toán).
Vậy: Giá 1 quả dừa 20 nghìn.
Giá 1 quả thanh long 5 nghìn.