Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
\(U_r^2+(U_L-U_C)^2=120^2\) (1)
\(U_r^2+U_L^2=160^2\) (2)
\(U_C=56\) (3)
Từ (1) suy ra: \(U_r^2+U_L^2+U_c^2-2U_LU_C=120^2\)
\(\Rightarrow 160^2+56^2-2.U_L.56=120^2\)
\(\Rightarrow U_L=128V\)
Thay vào (2) \(\Rightarrow U_r=96V\)
\(\Rightarrow r = \dfrac{96}{0,2}=480\Omega\)
Kết quả hơi lớn, bạn xem có phải I = 2 A không nhé.

Chọn D.
U = U R 2 + U L − U C 2 = 13 2 + 13 − 65 2 = 13 17 ≠ U
để cho cuộn dây có trở kháng r
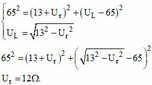
k = cos φ = U R + U r U = 13 + 12 65 = 5 13 .

Đáp án B
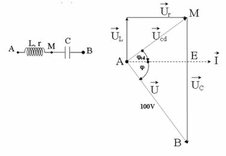
Sử dụng giản đồ vecto và định luật Ôm
Cách giải: Dựa vào biểu thức điện áp tức thời của cuộn dây và tụ, ta thấy ud sớm pha π 6 + 2 π 3 = 5 π 6 so với uC. Ta vẽ được giản đồ vecto như sau
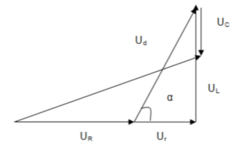
Từ giản đồ vecto thấy góc lệch giữa ud và uC là: α + π 2 = 5 π 6 ⇒ α = π 3
Từ phương trình điện áp ta có U d = 80 3 V ; U C = 40 V . Từ giản đồ vecto, ta có:
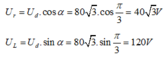
Ta có:
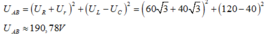
Hệ số công suất được xác định bởi:
k = cos φ = R + r Z - U R + U r U A B ≈ 0 , 908

Chọn A
Δ AEB : U r = AE = ABcos φ = 100 . 0 , 6 = 60 ( V ) EB = ABsin φ = AB 1 - cos 2 φ = 100 . 0 , 8 = 80 ( V ) Δ AEM ⇒ ME = AEtan φ cd = AE · sin φ os cos φ cot = AE 1 - cos 2 φ cd cos φ cot = 60 · 0 , 6 0 , 8 = 45 ( V )

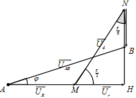
Biễu diễn vecto các điện áp. Với u d sớm pha hơn u C
một góc 150 độ → N ^ = 30 0 M ^ = 60 0
→ Trong tam giác vuông MHN, ta có
U r = U M N cos 60 0 = 40 3 U C = U M N sin 60 0 = 120 .
→ Hệ số công suất của đoạn mạch là
tan φ = U B H U R + U r = 120 − 40 60 3 + 40 3 ≈ 0 , 46
→ cos φ ≈ 0 , 908
Đáp án C

Đáp án C
+ Giả sử cuộn dây có điện trở thuần 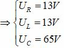
+ Ta có: ![]()
=> Cuộn dây có điện trở r
![]()


Đáp án B
Dựa vào biểu thức điện áp tức thời của cuộn dây và tụ, ta thấy udsớm pha ![]() so với uC . ta vẽ được giản đồ vecto như sau
so với uC . ta vẽ được giản đồ vecto như sau

Từ giản đồ vecto thấy góc lệch giữa ud và uClà:

Hệ số công suất được xác định bởi:
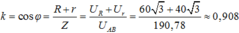

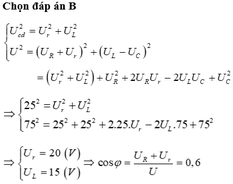
Ý a,,, vẽ hình ta thấy Ud=Uc=Um → tam giác đều → 2 góc= nhau=60o→ μm=30 →cos μm=1/2
Uc=120 Um=120 Ud=120
Ý B .. Có U2= (UR +Ur )2 +( UL--UC)2 và Ud2= Ur2+ UL2
thay số có : 752=(25 +Ur)2 +( UL--75)5 và 252= Ur2+UL2 →UL=\(\sqrt{25^2-Ur^2}\)
thế vào pt đầu ; 752= (25+Ur)2+ (\(\sqrt{25^2-Ur^2}\) --75)2
biến đổi đk pt ; 10Ur2 +50Ur--\(8\times25^2\) =0 → Ur= 20
Cos μm= \(\frac{Ur+UR}{U}=\frac{25+20}{75}=0,6\)