Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

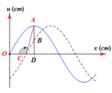
\(MA=6cm;MB=AB-MA=20-6=14cm\)
\(AM\perp MC\Rightarrow AC=\sqrt{AM^2+MC^2}=\sqrt{6^2+8^2}=10cm\)
\(BM\perp MC\Rightarrow BC=\sqrt{BM^2+MC^2}=\sqrt{14^2+8^2}=2\sqrt{65}cm\)
Xét một điểm N bất kì trên CM ta có: \(d_2-d_1=k\lambda\)
Hai nguồn dao động cùng pha:
\(\Rightarrow\left\{{}\begin{matrix}d_2-d_1=\left(k+0,5\right)\lambda\\BC-AC\le k\lambda\le BM-AM\end{matrix}\right.\)
\(\Rightarrow2\sqrt{65}-10\le k+0,5\le14-6\Rightarrow5,62\le k\le7,5\)
\(\Rightarrow k=\left\{6,5;7,5\right\}\)
Vậy có hai điểm cực tiểu trên CD.

Những điểm đứng yên là do hai sóng tới gặp nhau tại điểm đó ngược pha.

a) Vì hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc \(\dfrac{\pi}{2}\)
Khoảng cách giữa hai điểm là 360cm= \(\dfrac{3\lambda}{2}\) nên hai điểm này dao động ngược pha nhau độ lệch pha của chúng là π
b) Sau 0,1s sóng truyền được khoảng cách là 0,1.330 = 33m = \(\dfrac{55\lambda}{4}\)
Độ lệch pha là \(\dfrac{3\pi}{4}\)

Ta có: v = 20 cm/s = 0,2 m/s
Bước sóng là: λ= \(\frac{v}{f} = \frac{{0,2}}{{40}}\)= 0,005 (m)
Do: khoảng cách giữa 2 cực đại giao thoa cạnh nhau trên đoạn S1S2 = khoảng cách giữa 2 cực tiểu giao thoa cạnh nhau trên đoạn S1S2 = \(\frac{\lambda }{2}\).
⇒ Khoảng cách giữa hai điểm cực đại giao thoa trên đoạn S1S2 là:
d= \(\frac{\lambda }{2}\) = \(\frac{{0,005}}{2}\)= 0,0025 (m)