Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
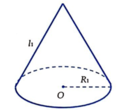
Gọi R 1 , h 1 lần lượt là bán kính đường tròn đáy và chiều cao của hình nón lúc đầu; R 2 , h 2 lần lượt là bán kính đường tròn đáy và chiều cao của hình nón sau khi tăng thể tích.
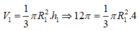
![]()
![]()
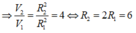
Diện tích xung quanh của hình nón lúc đầu: ![]()
Diện tích xung quanh hình nón khi tăng thể tích: ![]()
Diện tích phần giấy bạc cần tăng thêm: S = ( 12 13 - 15 ) π ( cm 2 )

Cỡ mẫu \(n = 3 + 8 + 7 + 3 = 21\).
Suy ra trung vị là \({x_{11}}\) thuộc nhóm [5; 10).

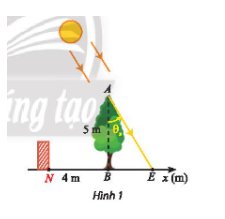
a, Xét tam giác ABE vuông tại B, ta có:
\(tan\theta_s\left(t\right)=\dfrac{BE}{AB}\Leftrightarrow BE=5tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]\)
b, Đồ thị của hàm số \(\theta_s=5tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]\)
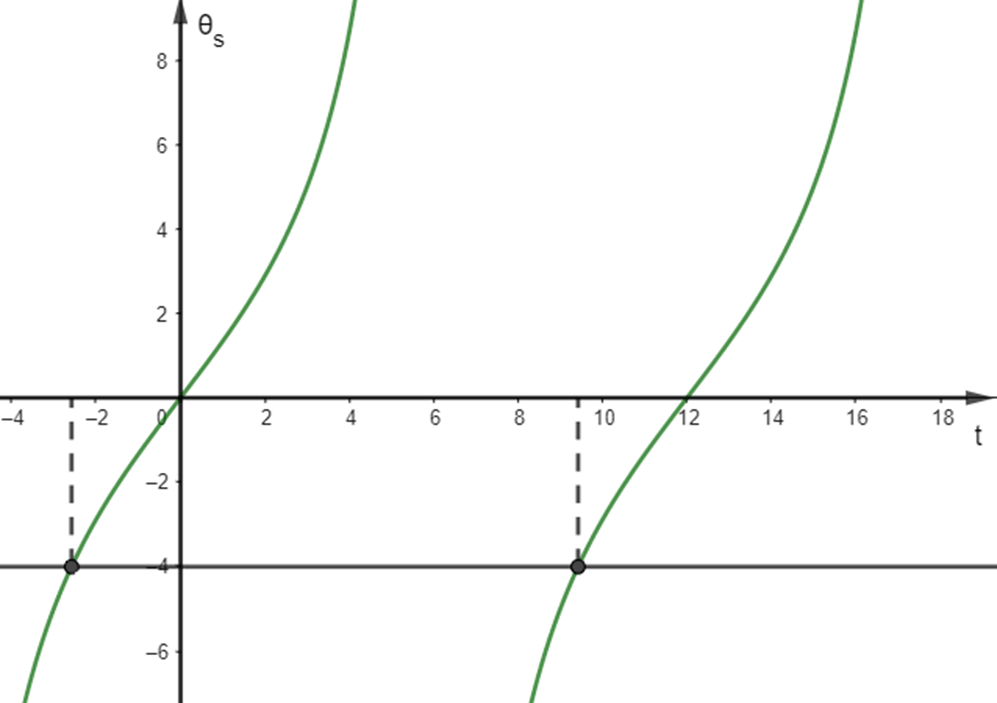
Dựa vào đồ thị hàm số, ta có:
\(\theta_s=5tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]< -4\\ \Leftrightarrow tan\left[\dfrac{\pi}{12}\left(t-12\right)\right]< -\dfrac{4}{5}\\ \Leftrightarrow\dfrac{\pi}{12}\left(t-12\right)< -0,67\\ \Leftrightarrow t< 9,4\)
Kết hợp điều kiện \(6< t< 18\Rightarrow6< t< 9,4\)
Vậy thời điểm bóng cây phủ qua hàng rào là 6 < t < 9,4.

Tham khảo:
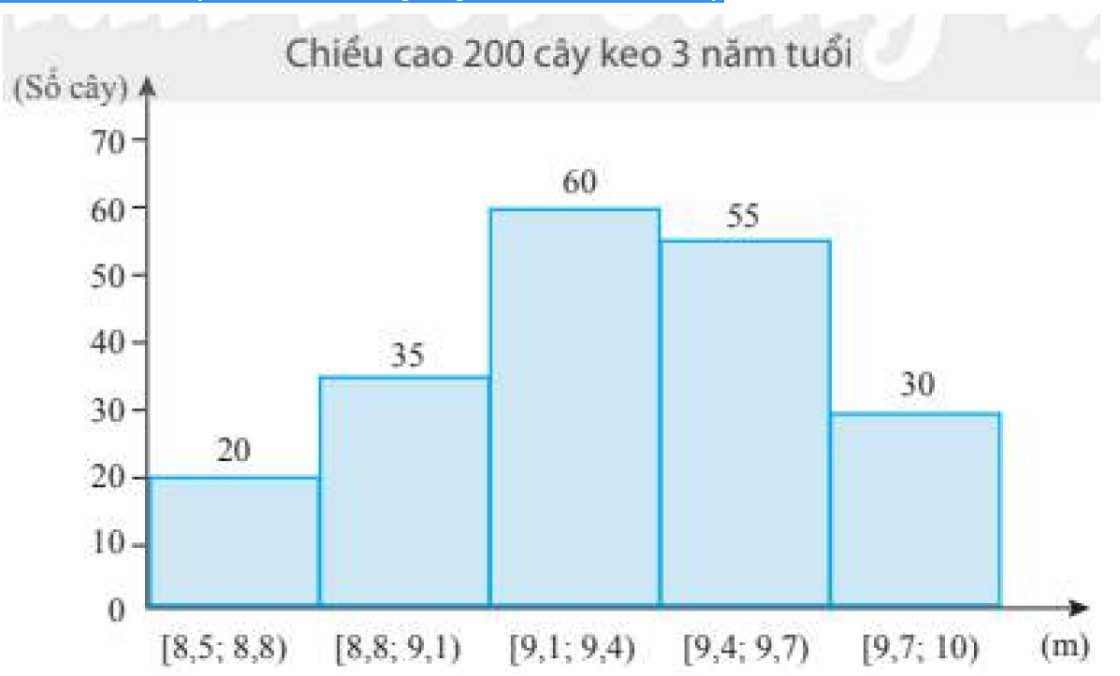
Chiều cao của 200 cây keo 3 năm tuổi được thống kê trong bảng sau:

Chiều cao của 200 cây keo 3 năm tuổi sau khi ghép nhóm là:
\(\bar x = \frac{{20.8,65 + 35.8,95 + 60.9,25 + 55.9,55 + 30.9,85}}{{200}} = 9,31\left( m \right)\)
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {9,1;9,4} \right)}\end{array}\).
Do đó: \({u_m} = 9,1;{n_{m - 1}} = 35;{n_m} = 60;{n_{m + 1}} = 55;{u_{m + 1}} - {u_m} = 9,4 - 9,1 = 0,3\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 9,1 + \frac{{60 - 35}}{{\left( {60 - 35} \right) + \left( {60 - 55} \right)}}.0,3 = 9,35\)
Vậy chiều cao của 200 cây keo 3 năm tuổi nhiều nhất là 9,35 mét.

Đáp án D
Gọi kích thước của đáy là a;b(a < b).Khi đó chiều cao của hố là h = 2a. Ta có: ![]()
Diện tích nguyên vật liệu cần dùng là:
![]()
![]()
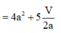
Xét hàm số:
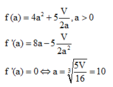
Xét hàm số:
Bảng biến thiên:
| a
|
0 10 + ∞ |
| f'(a)
|
- 0 + |
| f(a)
|
|
Vậy khi a = 10 thì hố ga được xây sẽ tiết kiệm nguyên liệu nhất.
![]()
![]()






Cây cao nhất với kiểu gene AABB có chiều cao là: \(100+5\cdot4=120\left(cm\right)\)