Question

[Nguyễn Trung Kiên]

nhờ các bạn giúp mình với

Answer 1

[Gấuu]

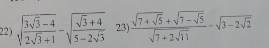
\(\sqrt{\dfrac{3\sqrt{3}-4}{2\sqrt{3}+1}}-\sqrt{\dfrac{\sqrt{3}+4}{5-2\sqrt{3}}}\)

\(=\sqrt{\dfrac{\left(3\sqrt{3}-4\right)\left(2\sqrt{3}-1\right)}{\left(2\sqrt{3}+1\right)\left(2\sqrt{3}-1\right)}}\)\(-\sqrt{\dfrac{\left(\sqrt{3}+4\right)\left(5+2\sqrt{3}\right)}{\left(5-2\sqrt{3}\right)\left(5+2\sqrt{3}\right)}}\)

\(=\sqrt{\dfrac{18-3\sqrt{3}-8\sqrt{3}+4}{\left(2\sqrt{3}\right)^2-1}}\)\(-\sqrt{\dfrac{5\sqrt{3}+6+20+8\sqrt{3}}{5^2-\left(2\sqrt{3}\right)^2}}\)

\(=\sqrt{\dfrac{22-11\sqrt{3}}{11}}\)\(-\sqrt{\dfrac{26+13\sqrt{3}}{13}}\)

\(=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}+1}-\sqrt{\left(\sqrt{3}\right)^2+2\sqrt{3}+1}\right)\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)

Answer 2

[Gấuu]

Ý còn lại đợi trưa nhá đi nấu cơm đã