Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S là tổng số hạt.
Theo đề bài:
p+e+n = S
mà p=e
=>2p + n = 34
n - p = 1
=> n= p+1
Thay p+1 vào phương trình 2p +n
ta có :
3p + 1 = 34
3p = 34 - 1
3p = 33
p = 33:3
p = e = 11
n = 11+1
n= 12
Cứ ghi thế này vào bài kiểu gì cũng ăn được full điểm. =))

Câu a)
\(\left\{{}\begin{matrix}2P+N=34\\2P-N=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}P=E=Z=11\\N=12\end{matrix}\right.\\ KHHH:Natri\left(KHHH:Na\right)\)
Câu b)
\(\left\{{}\begin{matrix}2P+N=21\\2P=2N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2P+N=21\\P=N\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}P=E=Z=7\\N=7\end{matrix}\right.\Rightarrow Nitơ\left(KHHH:N\right)\)
Câu c)
\(\left\{{}\begin{matrix}2P+N=58\\2P-N=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}P=E=Z=19\\N=20\end{matrix}\right.\\ \Rightarrow Kali\left(KHHH:K\right)\)

gọi só hạt proton, electron và notron lần lượt là p,e,n
ta có \(p=e\)
\(=>p+e=2p\)
Theo đề ta có:
\(\left\{{}\begin{matrix}2p+n=52\\n-p=1\end{matrix}\right.\)
\(=>p=17\) và \(n=18\)
=> số hạt proton, electron và notron lần lượt là 17,17,18

\(\begin{cases} p=e\\ p+e+n=34\\ n-p=1 \end{cases} \Rightarrow \begin{cases} p=e\\ 2p+n=34\\ n-p=1 \end{cases}\Rightarrow \begin{cases} p=e=11\\ n=12 \end{cases}\)
Vậy \(p=11\)

Ta có: n + p + e = 34
mà p = e, nên: 2p + n = 34
Vì số hạt mang điện nhiều hơn số hạt ko mang điện là 10 hạt nên: 2p - n = 10
=> Ta có HPT: \(\left\{{}\begin{matrix}2p+n=34\\2p-n=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=24\\2p-n=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=12\\p=11\end{matrix}\right.\)
Vậy n = 12 hạt, p = e = 11 hạt.

Bài 1:
Ta có: p = e
=> p + e + n = 34 <=> 2p + n = 34 (1)
=> 2p - n = 10 (2)
Từ (1) và (2) => p = e = 11; n = 12
Bài 1:
Ta có: \(\left\{{}\begin{matrix}p+n+e=34\\p+e-n=10\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2p+n=34\\2p-n=10\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=e=11\\n=12\end{matrix}\right.\)
Bài 2:
Ta có: \(\left\{{}\begin{matrix}p+e+n=60\\p=n\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2p+n=60\\p-n=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=20=e\\n=20\end{matrix}\right.\)
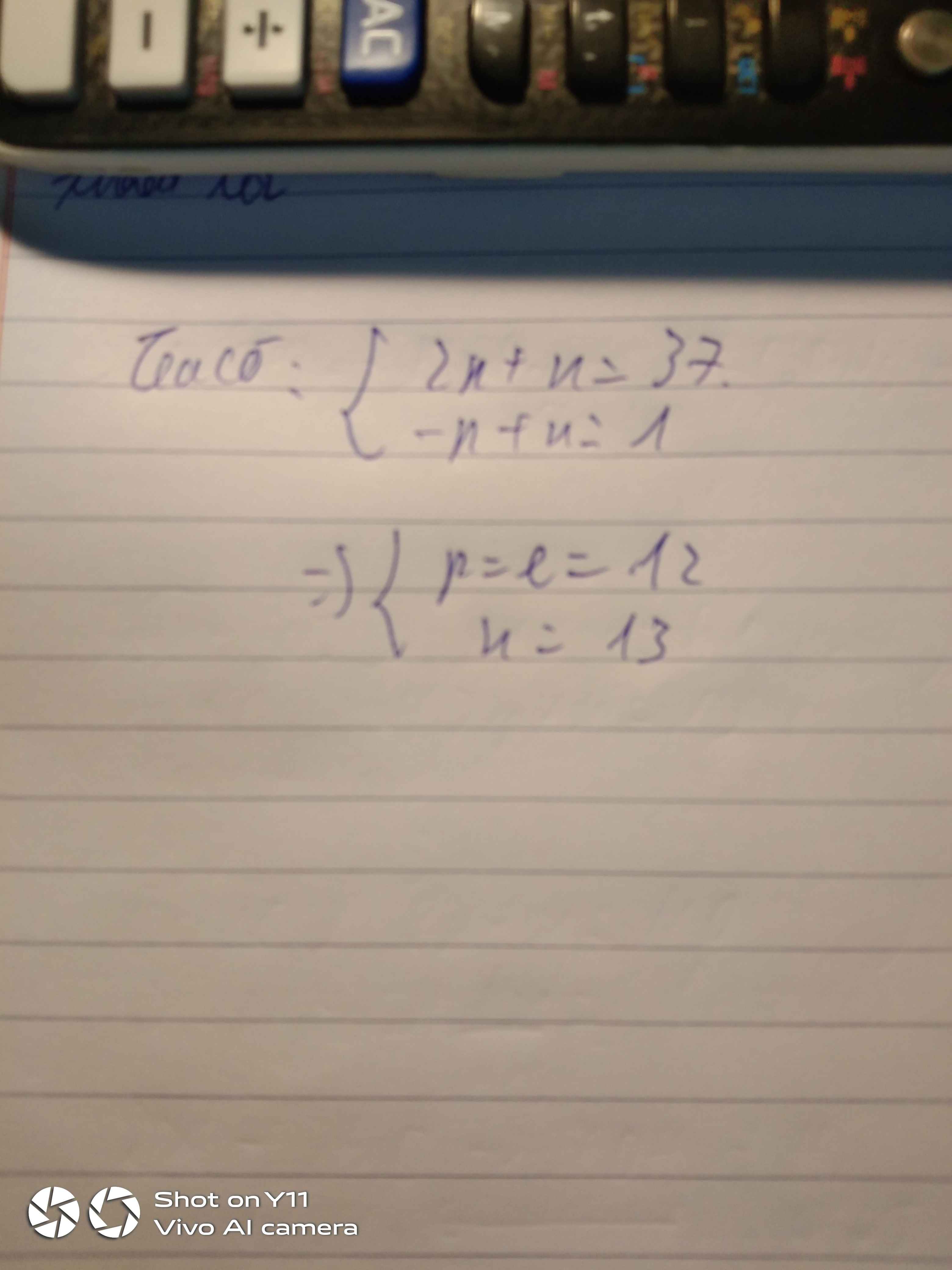
Chọn C