Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi t là tổng thời gian ô tô đi hết quãng đường
Ta có: 15m/s = 54km/h
Quãng đường ô tô đi trong \(\dfrac{1}{2}\) thời gian đầu là:
\(s_1=v_1t_1=30\cdot\dfrac{1}{2}t=15t\)
Quãng đường ô tô đi trong \(\dfrac{1}{2}\) thời gian sau là:
\(s_2=v_2t_2=54\cdot\dfrac{1}{2}t=27t\)
Vận tốc trung bình của ô tô là:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{15t+27t}{t}=42\) (km/h)
Vậy...

B
Gọi nửa thời gian là t các quãng đường trong nửa thời gian là:
S 1 = v 1 t = 30t ; S 2 = v 2 t = 15t
Vận tốc trung bình trên cả đoạn đường là:
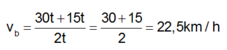

gọi s là quãng đường AB
s1,s2,s3 lần lượt là từng quãng đường mà xe di chuyển:
s1 = \(\frac{1}{3}s\)
=> s2 + s3 = \(\frac{2}{3}s\)
Thời gian xe di chuyển trong \(\frac{1}{3}\) quãng đường là:
t1 = \(\frac{s_1}{v_1}=\frac{s}{3.40}=\frac{s}{120}\)
Gọi t' là thời gian đi ở quãng đường (\(\frac{2}{3}s\)) còn lại:
Trong \(\frac{2}{3}\) thời gian đầu, xe đi được quãng đường là
s2 = \(\frac{2}{3}t'.v_2=\frac{2}{3}.t'.45=30t'\)
Quãng đường xe đi được trong thời gian còn lại là:
s3=\(\frac{1}{3}t'.v_3=\frac{1}{3}t'.30=10t'\)
Mặt khác ta có
s2 + s3 = \(\frac{2}{3}s\)
=> 30t' + 10t' = \(\frac{2}{3}s\)
=> 40t'=\(\frac{2}{3}s\)
=> t'=\(\frac{s}{60}\)
Vận tốc trung bình của xe là:
\(v_{tb}=\frac{s}{t+t'}=\frac{s}{\frac{s}{120}+\frac{s}{60}}=\frac{1}{\frac{1}{120}+\frac{1}{60}}=40\)(km/h)

Một xe đi từ A về B, trong nửa quãng đương đầu, xe chuyển động với vận tốc v1= 40 km/h. Trên nửa quãng đường sau xe chuyển động thành 2 giai đoạn: nửa thời gian đầu vận tốc v2 = 45 km/h, thời gian còn lại đi với vận tốc v3 = 30 km/h. Tính vận tốc trung bình của xe trên cả quãng đường AB.
Đề phải như này mới đúng

Gọi S(km) là quãng đường AB(S>0)
\(10\left(\dfrac{m}{s}\right)=36\left(\dfrac{km}{h}\right)\)
\(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{S}{2.40}=\dfrac{S}{80}\left(h\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2.36}=\dfrac{S}{72}\left(h\right)\end{matrix}\right.\)
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{80}+\dfrac{S}{72}}=\dfrac{S}{S.\dfrac{19}{720}}\approx38\left(\dfrac{km}{h}\right)\)
Đáp án A