Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo tại đây nha, chúc bn học tốt
http://diendan.hocmai.vn/threads/vat-ly-8-bai-chuyen-dong.329755/
Ta có: Vận tốc trung bình = Tổng quãng đường : Tổng thời gian
Gọi chiều dài mỗi đoạn là a (đơn vị là m)
=> t1 = \(\frac{x}{12}\)
=> t2 = \(\frac{x}{8}\)
=> t3 = \(\frac{x}{16}\)
=> Tổng thời gian 13/48\(x\)
Vận tốc trung bình là : = Tổng quãng đường : Tổng thời gian = 3\(x\) : [(13/48)x] = 11,0769 \(\approx\) 11,08

Theo đề bài ta có:
\(S_1=S_2=S_3=\frac{S}{3}\)
Lại có: \(t_1=\frac{S_1}{v_1}=\frac{S}{3}.v_1\)
Và: \(t_2=\frac{S_2}{v_2}=\frac{S}{3}.v_2\)
Tương tự: \(t_3=\frac{S_3}{v_3}=\frac{S}{3}.v_3\)
Vận tốc trung bình là:
\(v_{tb}=\frac{S_1+S_2+S_3}{t_1+t_1+t_3}=\frac{S}{\frac{S}{3v_1}+\frac{S}{3v_2}+\frac{S}{3v_3}}=\frac{3}{\frac{1}{v_1}+\frac{1}{v_2}+\frac{1}{v_3}}\approx6,55\) (m/s)

Gọi chiều dài mỗi đoạn đường là s
\(v_{tb}=\dfrac{3s}{\dfrac{s}{12}+\dfrac{s}{8}+\dfrac{s}{16}}=\dfrac{3s}{\dfrac{4s+6s+3s}{48}}=\dfrac{3s}{\dfrac{13s}{48}}\approx11,07\left(\dfrac{m}{s}\right)\)
Một ô tô chuyển động trên chặng đường gồm ba đoạn liên tiếp cùng chiều dài. Vận tốc của xe trên mỗi đoạn là V1 = 12m/s; v2 = 8m/s; v3 = 16m/s. Tính vận tốc trung bình của ôtô cả chặng đường.
\(V_{tb}=\dfrac{V_1+V_2+V_3}{3}=\dfrac{12+8+16}{3}=12\)(m/s)

a, \(t_1=\dfrac{S}{\dfrac{3}{12}}=\dfrac{S}{36}\)
\(t_2=\dfrac{S}{\dfrac{3}{8}}=\dfrac{S}{24}\)
\(t_3=\dfrac{S}{\dfrac{3}{16}}=\dfrac{S}{48}\)
\(\Rightarrow v_{tb}=\dfrac{S}{t_1+t_2+t_3}=\dfrac{S}{\dfrac{S}{36}+\dfrac{S}{24}+\dfrac{S}{48}}=\dfrac{1}{\dfrac{1}{36}+\dfrac{1}{24}+\dfrac{1}{48}}\approx11,1\left(km/h\right)\)
b, chiều dải cả quãng đường
\(39,96.3=119,88\left(km\right)\)
thời gian đi hết cả quãng đường là
\(t=\dfrac{S}{v}=\dfrac{119,88}{11,1}=10,8\left(h\right)\)

2) Gọi S là chiều dài của 1 đoạn đường.
Thời gian ô tô đi hết đoạn 1 là : \(t_1=\frac{S}{v_1}=\frac{S}{12}\left(s\right)\)
Thời gian ô tô đi hết đoạn 2 là: \(t_2=\frac{S}{v_2}=\frac{S}{8}\left(s\right)\)
Thời gian ô tô đi hết đoạn 3 là : \(t_3=\frac{S}{v_3}=\frac{S}{16}\left(s\right)\)
Vận tốc trung bình của ô tô trên cả chặng đường :
\(v_{tb}=\frac{S+S+S}{t_1+t_2+t_3}=\frac{3S}{\frac{S}{12}+\frac{S}{8}+\frac{S}{16}}\)
\(\Leftrightarrow v_{tb}=\frac{3}{\frac{1}{12}+\frac{1}{8}+\frac{1}{16}}=\frac{3}{\frac{13}{48}}\)
\(\Rightarrow v_{tb}=\frac{144}{13}\left(\frac{m}{s}\right)\)
1) Gọi S là chiều dài quãng đường người đó phải đi
Thời gian người đó đi hết nửa quãng đường đầu: \(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{2.12}=\frac{S}{24}\left(h\right)\)
Thời gian người đó đi hết quãng đường còn lại: \(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\left(h\right)\)
Theo bài ra ta có:
\(v_{tb}=\frac{S_1+S_2}{t_1+t_2}=\frac{S}{\frac{S}{24}+\frac{S}{2v_2}}=\frac{2.24.v_2}{24+v_2}=\frac{48.v_2}{24+v_2}\)
\(\Leftrightarrow8=\frac{48v_2}{24+v_2}\Leftrightarrow8\left(24+v_2\right)=48v_2\)
\(\Leftrightarrow192+8v_2=48v_2\Leftrightarrow40v_2=192\)
\(\Rightarrow v_2=\frac{192}{40}=4,8\left(\frac{km}{h}\right)\)

Gọi s là chiều dài nửa quãng đường
Thời gian đi hết nửa quãng đường đầu với vận tốc v1 là t1=sv1t1=sv1 (1)
Thời gian đi hết nửa quãng đường còn lại với vận tốc v2 là t2=sv2t2=sv2 (2)
Vận tốc trung bình của người đi xe đạp trên quãng đường là vtb=2st1+t2vtb=2st1+t2 (3)
Kết hợp (1); (2); (3) có: 1v1+1v2=2vtb1v1+1v2=2vtb
Thay số vtb = 8km/h; v1 = 12km/h
Vận tốc trung bình của người đi xe ở nửa quãng đường sau là v2 = 6km/h
Gọi s là chiều dài nửa quãng đường
Thời gian đi hết nửa quãng đường đầu với vận tốc v1 là t1=s/v1 (1)
Thời gian đi hết nửa quãng đường còn lại với vận tốc v2 là t2=s/v2 (2)
Vận tốc trung bình của người đi xe đạp trên quãng đường là vtb=2s/t1+t2 (3)
Kết hợp (1); (2); (3) có: 1/v1+1/v2=2/vtb
Thay số vtb = 8km/h; v1 = 12km/h
Vận tốc trung bình của người đi xe ở nửa quãng đường sau là v2 = 6km/h
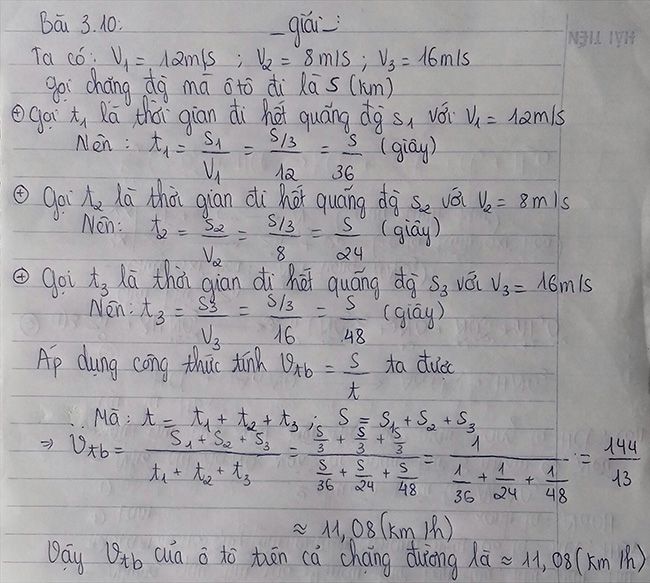
Gọi S(m) là độ dài mỗi quãng đường (S>0)
\(\left\{{}\begin{matrix}t_1=\dfrac{S}{v_1}=\dfrac{S}{12}\left(s\right)\\t_2=\dfrac{S}{v_2}=\dfrac{S}{8}\left(s\right)\\t_3=\dfrac{S}{v_3}=\dfrac{S}{6}\left(s\right)\end{matrix}\right.\)
\(v_{tb}=\dfrac{3S}{t_1+t_2+t_3}=\dfrac{3S}{\dfrac{S}{12}+\dfrac{S}{8}+\dfrac{S}{6}}\)
\(=\dfrac{S}{\dfrac{3}{8}S}=\dfrac{1}{\dfrac{3}{8}}=\dfrac{8}{3}\left(m/s\right)\)