Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Thể tích của cốc nước hình trụ là
\(V_{trụ}=\pi r^2h=\pi.\dfrac{d^2}{4}.h=\pi.\dfrac{8^2}{4}.9=144\pi\left(cm^3\right)\)
Thể tích của viên bi hình cầu là
\(V_{cầu}=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi.3^3=12\pi\left(cm^3\right)\)
Vì khi thả viên bi vào cốc nước đang chứa đầy nước thì lượng nước trào ra ngoài bằng đúng thể tích của viên bi nên lượng nước còn lại trong cốc là \(144\pi-12\pi=132\pi\left(cm^3\right)\approx414,48\left(cm^3\right)=414,48\left(ml\right)\)
Thể tích của cốc nước hình trụ là
Thể tích của viên bi hình cầu là
Vì khi thả viên bi vào cốc nước đang chứa đầy nước thì lượng nước trào ra ngoài bằng đúng thể tích của viên bi nên lượng nước còn lại trong cốc là
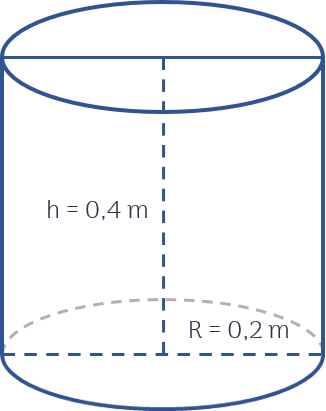
- Bán kính đáy của bồn chứa xăng là: 2,2/2=1,1 (m)
- Diện tích toàn phần của bồn chứa xăng là:
\(S_{tp}=S_{xq}+2S_{đáy}=C_{đáy}.h+2S_{đáy}=2\pi\times1,1\times3,5+2\pi\times1,1^2=10,12\pi\left(m^2\right)\)
- Số kg sơn cần dùng để sơn bề mặt ngoài của bồn chứa xăng là:
\(\dfrac{10,12\pi}{8}\approx\dfrac{10,12\times3,14}{8}\approx3,97\left(kg\right)\)
Bk đáy = \(r=\dfrac{40}{2}=20\left(cm\right)\)
Cần dùng tối thiếu số ` m^2 ` là
\(S_{xq}=2\pi rh=2.\pi.20.60=2400\left(cm^2\right)=0,24\left(m^2\right)\)
Thể tích chiếc thùng hình trụ đó là
\(V=\pi r^2h=\pi.20^2.60=24000\left(cm^3\right)=24l\)
Vậy thùng đó đựng đc nhiều nhất 24l và số ` m^2 ` tôn thùng đó cần dùng là 0,24 ` m^2 `
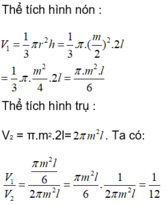
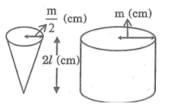
Vậy khi múc đầy nước vào hình nón và đổ vào hình trụ (Không chứa gì cả) thì độ cao của nước trong hình trụ là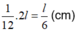 
Vậy chọn đáp án A
nghe như lý ấy nhờ @@
diện tích mặt đyas bình là : \(S=6^2\pi=36\pi\left(cm^2\right)\)
=> thể tích viên bi : \(V=S.h=36\pi.1=36\pi\left(cm^3\right)\)
\(\Leftrightarrow\dfrac{4}{3}\pi r^3=36\pi\Leftrightarrow r=\sqrt[3]{27}=3\left(cm\right)\)
a, Tính lượng nước \(\left(m^3\right)\)anh Minh đổ vào hố sau mỗi làn gánh ( ghi kết quả làm tròn đến 2 chữ số thập phân )
Biết trong quá trình gánh nước thì lượng nước bị hao hụt khoảng 10% nên
Công thức tính thể tích hình trụ là : \(V=ttR^2h\)
Thể tích của 2 thùng nước mỗi lần anh Minh gánh được là :
\(V_1=2ttR^2h=2tt\times0,0^2\times0,4=0,032tt\left(m^3\right)\)
Trong quá trình gánh , lượng nước hao hụt 10% nên lượng nước thực tế anh Minh đổ vào hồ sau mỗi lần gánh là :
\(V=0,032tt\times90\%=0,09\left(m^3\right)\)
b, Thể tích của hồ nước hình chữ nhật là :
\(V_0=2\times2\times1=4\left(m^3\right)\)
Số lần ít nhất anh Minh cần gánh để đổ đầy hồ nước là :
\(n=[\frac{V_0}{V}]+1=[\frac{4}{0,09}]+1=44+1=45\)Lần
Diện tích tôn cần dùng:
\(S=\Pi r^2+2\Pi rh=\Pi.1^2+2.\Pi.1.3=7\Pi\left(dm^2\right)\)
Thể tích của ba viên bi:
\(3.\dfrac{4}{3}\pi.1^3=4\pi\left(cm^3\right)\)
Tổng thể tích nước và 3 viên bi:
\(4\pi+10.\pi.3^2=94\pi\left(cm^3\right)\)
Chiều cao mực nước:
\(h=\dfrac{94\pi}{\pi.3^2}\approx10,44\left(cm\right)\)