Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Số đó cho biết khối lượng của hộp sữa và lượng gạo đó đúng bằng 397g.
2.Mình không biết giải thích làm sao cả câu 3 nữa

Ta lần lượt đánh dấu các gói mì từ 1 đến 6 và lấy ra tương ứng: thùng 1 lấy 1 gói ; thùng 2 lấy 2 gói ;....; thùng 6 lấy 6 gói rồi bỏ tất cả lên cân
Như vậy tổng khối lượng của các gói mì lấy ra là:
m = (1 + 2 + 3 +4 + 5 + 6).m0 = 21.m0 = 21.50 = 1050 (g) (m0 là khối lượng mì chuẩn)
- Do gói mì kém chất lượng nhẹ hơn gói mì chuẩn là 50 - 45 = 5g nên khi ta cân nếu khối lượng thực tế nhỏ hơn tổng khối lượng m là 5g ; 10g ; 15g ; 20g ; 25g ; 30g thì tương ứng là thùng mì số 1;2;3;4;5;6 kém chất lượng.

* Chứng minh
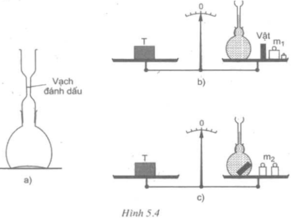
Lần cân thứ nhất: mT = mb + mn + mv + m1 (1).
Lần cân thứ hai: mT = mb + (mn – mn0) + mv + m2 (2).
Trong phương trình (1), mn là khối lượng của nước chứa trong bình tới vạch đánh dấu, mb là khối lượng vỏ bình, mv là khối lượng vật.
Trong phương trình (2), mn0 là khối lượng của phần nước bị vật chiếm chỗ.
Vì mT là không thay đổi nên từ (1), (2) ta có:
mb + mn + mv + m1 = mb + (mn – mn0) + mv + m2
↔ mn0 = m2 – m1.
Vì 1 gam nước nguyên chất có thể tích là 1cm3, nên số đo khối lượng mn theo đơn vị gam là số đo có thể tích của phần nước bị vật chiếm chỗ theo đơn vị cm3.
Thể tích của phần nước bị vật chiếm chỗ chính là thể tích của vật. Do đó thể tích của vật tính ra cm3 có độ lớn bằng V = m2 – m1.
* Cách xác định vật thể như trên chính xác hơn cách xác định bằng bình chia độ, đo khối lượng bằng cân Rôbécvan chính xác hơn đo thể tích bằng bình chia độ do:
+ GHĐ của cân Rôbécvan nhỏ hơn GHĐ của bình chia độ rất nhiều.
+ Cách đọc mực nước ở bình chia độ khó chính xác hơn cách theo dõi kim của cân ở vị trí cân bằng. Mặt khác, cách cân hai lần như trên loại trừ được những sai số do cân cấu tạo không được tốt, chẳng hạn hai phần của đòn cân không thật bằng nhau về chiều dài cũng như khối lượng.