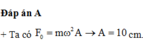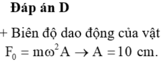Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực kéo về
\(F = -kx= -k.A.\cos (\omega t +\varphi)\)
So sánh với phương trình \(F=-0.8\cos 4t(N)\) => \(\omega = 4\)(rad/s) và \( k.A = 0,8 \)
\(=> m\omega^2 A = 0,8 => A = \frac{0,8}{m\omega^2}= \frac{0,8}{0,5.4^2}= 0,1 m = 10cm.\)

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Lực kéo về tác dụng lên vật có độ lớn cực đại là \(F_{max}=kA= m(2\pi f)^2 A = 0,1.4.10.5^2.0,04 = 4N.\)

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

Độ cứng của lò xo là:
\(k=\frac{2W}{A^2}=\frac{2X0,2}{0,1^2}=40\left(N/m\right)\)
Tần số góc là:
\(\omega=\frac{2\pi}{T}=\frac{2\pi}{0,5}=4\left(rad/s\right)\)
Khối lượng của vật là:
\(m=\frac{k}{\omega^2}=\frac{40}{\left(4\pi\right)^2}=0,25\left(kg\right)=250\left(g\right)\)