Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc dòng nước = vận tốc bè trôi = a km/h (a>0). Gọi vận tộc ca nô là x km/h (x>a); => vận tốc xuôi dong là x+a, còn ngược dòng là x-a. Do Ca nô xuôi dòng 144 km thì quay trở về A ngay , cả đi lẫn về hết 21giờ nên ta có phương trình 144/(x+a) + 144/(x-a) = 21 (1) và 144/(x+a) + (144-36)/(x-a) = 36/a <=> 144/(x+a) + 108/(x-a) = 36/a. Quy đồng rồi chuyển vế ta tìm được x=7a, thay x=7a vào (1) ta được 144/8a + 144/6a = 21 <=> 42/a = 21 <=> a=2 => x=14 (thoả mãn ĐK x>a>0). Vậy vận tốc canô là 14km/h còn vận tốc dòng nước là 2km/h. Mình nghĩ nếu bỏ phương trình (1) đi chắc cũng không sao
vậy còn cái này sao ???????

Gọi x(km/h) là vận tốc thực của thuyền máy
ĐK:x\(\ge\)2
Vận tốc lúc xuôi dòng: x+2 km/h
Vận tốc lúc ngược dòng: x-2 km/h
Thời gian lúc xuôi dòng từ A đến B: \(\frac{42}{x+2}\) h
Thời gian lúc ngược dòng từ B về A: \(\frac{42}{x-2}\) h
Vì thời gian lúc ngược dòng nhiều hơn thời gian xuôi dòng là 1 h 12' =\(\frac{6}{5}\)h nên ta có phương trình:
\(\frac{42}{x-2}-\frac{42}{x+2}=\frac{6}{5}\)
=>6x2-864=0
Giải phương trình ta được: x1=12(nhận) ; x2=-12(loại)
Vậy vận tốc xuôi dòng là 14 km/h vận tốc ngược dòng là 10 km/h

Tham khảo:
Gọi \(\overrightarrow a ,\overrightarrow b \) lần lượt là vectơ vận tốc riêng của ca nô A và B (cùng độ lớn).
Vì ca no A chạy xuôi dòng nên ngoài vận tốc riêng của ca nô, ca nô A còn được đẩy đi bởi vận tốc của dòng nước. Do đó vectơ vận tốc thực của cano A cùng hướng với vectơ \(\overrightarrow a \) và có độ lớn bằng tổng của vận tốc riêng và vận tốc dòng nước, là 18 km/h.
Ngược lại, ca nô đi ngược dòng nên bị cản lại một phần bởi dòng nước. Vì vận tốc của dòng nước nhỏ hơn vận tốc riêng của cano B nên vectơ vận tốc thực của cano B cùng hướng với vectơ \(\overrightarrow b \) và có độ lớn bằng hiệu giữa vận tốc riêng và vận tốc dòng nước, là 12 km/h.
Ta biểu diễn vận tốc thực của ca nô A và ca nô B như sau:
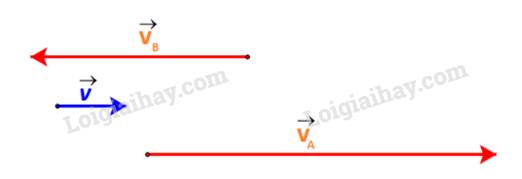
b) Dễ thấy:
Các vectơ \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \) đều có giá song song nên chúng cùng phương với nhau.
Ca nô A đi xuôi dòng nên vectơ vận tốc thực của ca nô A cùng hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_A}} \) cùng hướng.
Ca nô A đi ngược dòng nên vectơ vận tốc thực của ca nô B ngược hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_B}} \) ngược hướng.
Chú ý khi giải
Vận tốc riêng của cano là vận tốc của cano khi dòng nước đứng im.
Vận tốc thực của cano là vận tốc của cano khi kết hợp với dòng nước (đang chảy)

Gọi vận tốc thật của cano là x(km/h)
ĐK: x\(\ge\)5
Vận tốc xuôi dòng x+5 km/h
Vận tốc ngược dòng: x-5 km/h
Thời gian xuôi dòng: \(\frac{90}{x+5}\) h
Thời gian ngược dòng: \(\frac{90}{x-5}\) h
Theo đề ta có PT:
\(\frac{90}{x+5}+\frac{90}{x-5}=\frac{15}{2}\)
=>15x2-360x-375=0
Giải PT ta được: x1=25(nhận) ; x2=-1 (loại)
Vậy vận tốc của cano khi xuôi dòng là: 30 km/h

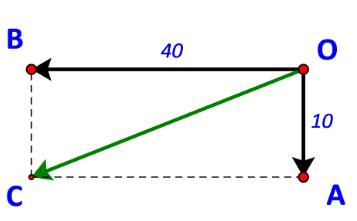
Gọi O là vị trí của ca nô.
Vẽ \(\overrightarrow {OA} \) là vận tốc dòng nước (chảy từ phía bắc xuống phía nam),
\(\overrightarrow {OB} \) là vận tốc riêng của ca nô (chuyển động từ phía đông sang phía tây)
Khi đó vecto vận tốc của ca nô so với bờ sông là vecto \(\overrightarrow {OA} + \overrightarrow {OB} \)
Gọi C là đỉnh thứ tư của hình bình hành OACB, ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \)
Xét tam giác OBC vuông tại B ta có:
BC = 40; BC = OA = 10.
\( \Rightarrow OC = \sqrt {O{B^2} + B{C^2}} = 10\sqrt {17} \)
Vậy vận tốc của ca nô so với bờ sông là \(10\sqrt {17} \) km/h.

Vì ca-nô đi từ A đến B mất 2 giờ, nên trong 1 giờ ca-nô đi được \(\frac{1}{2}\) AB.
Ca-nô đi từ B đến A mất 3 giờ, nên trong 1 giờ ca-nô đi được \(\frac{1}{3}\) AB.
Vận tốc ca-nô từ A đến B hơn vận tốc ca-nô từ B đến A là:
\(\frac{1}{2}-\frac{1}{3}=\frac{1}{6}\) (quãng AB).
Vì hiệu vận tốc cano xuôi dòng và vận tốc cano ngược dòng bằng 2 lần
Vận tốc dòng nước nên 1 giờ khóm bèo trôi được là:
\(\frac{1}{6}:2=\frac{1}{12}\) (quãng AB).
Vậy thời gian để khóm bèo trôi từ A đến B là 12 giờ.
Vì cano đi từ A đến B mất 2 giờ nên trong 1 giờ cano đi được 1/2 AB.
Cano đi từ B đến A mất 3 giờ nên trong 1 giờ cano đi được 1/3 AB.
Vận tốc cano từ A đến B hơn vận tốc cano từ B đến A là: 1/2 - 1/3 = 1/6 (quãng AB).
Vì hiệu vận tốc cano xuôi dòng và vận tốc cano ngược dòng bằng 2 lần vận tốc dòng nước nên 1 giờ khóm bèo trôi được là:
1/6 : 2 = 1/12 (quãng AB).
Vậy thời gian để khóm bèo trôi từ A đến B là 12 giờ.

Tỉ số thời gian đi và về là : \(\frac{t1}{t2}=\frac{5}{3}=\frac{v1}{v2}=\frac{3}{5}\)
Do thời gian và vận tốc của ca nô lúc đi và về trên cùng quãng đường tỉ lệ nghịch với nhau nên nếu ta biểu diễn vận tốc của ca nô lúc đi là 3 phần thì lúc về là 5 phần như thế .
Ta có
Vận tốc đi : 3 phần
Vận tốc về 5 phần bằng nhau trong đó hơn vận tốc đi 2 phần là 14 km (Mình không vẽ được sơ đồ nên biểu diễn bằng lời)
Vận tốc ca nô đi là :
( 14:2) x 3 = 21 ( km/ giờ )
Độ dài quãng sông là :
21 x 5 = 105( km)

Gọi thời gian chiếc thuyền đi từ A đến B là x
Thời gian chiếc thuyền đi ngược từ B về A là y.
Ta có: 4,5km=\(\frac{1}{2}\)của 9km
Do đó thời gian chiếc thuyền đi ngược từ B về A gấp đôi thời gian chiếc thuyền đi từ A đến B.
=> y = 2x
Mà x + y = 1h45p= 105 phút
Thay y = 2x ta có
x+2x=3x=105 phút
x=105 phút : 3
x=35 phút =\(\frac{7}{12}\) giờ
Vậy độ dài quãng đường là:
\(9x\frac{7}{12}=5,25\left(km\right)\)
Đáp số: 5.25 km
