K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HL
1
31 tháng 8 2017
B C' A' A
Ta có : A'BC' + ABC' = 180\(^0\)
=> Theo từng trường hợp , A'BC' + ABC' = 180\(^0\)
17 tháng 5 2022
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC
Thông cảm mk bị cận!
Cậu nào giải được giải giúp tớ với 
Tớ camon người giúp tớ nhiều lắm ạ 
Help me
TT
7 tháng 10 2017
\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
7 tháng 10 2017
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)
16 tháng 3 2017
vòng 18 đó bạn
mình cũng thi nè
chúc bạn thi tốt nha
16 tháng 3 2017
thi v18 bn à, mk ở bảng A thi hôm qua r (15/3) còn B thi 20/3
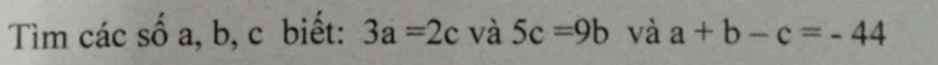
\(3a=2c\Leftrightarrow\dfrac{a}{2}=\dfrac{b}{3}\Leftrightarrow\dfrac{a}{10}=\dfrac{b}{15};5c=9b\Leftrightarrow\dfrac{b}{5}=\dfrac{c}{9}\Leftrightarrow\dfrac{b}{15}=\dfrac{c}{27}\\ \Leftrightarrow\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}=\dfrac{a+b-c}{10+15-27}=\dfrac{-44}{-2}=22\\ \Leftrightarrow\left\{{}\begin{matrix}a=220\\b=330\\c=594\end{matrix}\right.\)
Ta có: 3a=2c, 5c=9b
\(\Rightarrow\dfrac{a}{2}=\dfrac{b}{3},\dfrac{c}{9}=\dfrac{b}{5}\)
\(\Rightarrow\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}\)
Áp dụng t/c của DTSBN, ta có:
\(\dfrac{a}{10}=\dfrac{b}{15}=\dfrac{c}{27}=\dfrac{a+b-c}{10+15-27}=\dfrac{-44}{-2}=22\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{10}=22\\\dfrac{b}{15}=22\\\dfrac{c}{27}=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=220\\b=330\\c=594\end{matrix}\right.\)