K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 10 2020
a/
\(\left(m+1\right)^2+\left(m-1\right)^2\ge\left(2m+3\right)^2\)
\(\Leftrightarrow2m^2+12m+7\le0\)
\(\Leftrightarrow\frac{-6-\sqrt{22}}{2}\le m\le\frac{-6+\sqrt{22}}{2}\)
b/ \(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m-1\right)^2+4m\ge m^4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m^4-\left(m+1\right)^2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m^2+m+1\right)\left(m^2-m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow0\le m\le\frac{1+\sqrt{5}}{2}\)
c/ \(\Leftrightarrow\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x+\frac{1}{2}=m\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)+\frac{1}{2}=m\)
Do \(-\frac{1}{2}\le sin\left(2x-\frac{\pi}{3}\right)\le\frac{3}{2}\Rightarrow-\frac{1}{2}\le m\le\frac{3}{2}\)
MT
0
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2020
Miền xác định của hàm là miền đối xứng
\(f\left(-x\right)=\frac{m.cos\left(-x\right)}{tan\left(-3x\right)}+\left(m+1\right)\left|sin\left(-2x\right)\right|\)
\(=-\frac{mcosx}{tan3x}+\left(m+1\right)\left|sin2x\right|\)
Hàm lẻ khi và chỉ khi \(f\left(-x\right)=-f\left(x\right)\) với mọi x thuộc TXĐ
\(\Leftrightarrow-\frac{mcosx}{tan3x}+\left(m+1\right)\left|sin2x\right|=-\frac{mcosx}{tan3x}-\left(m+1\right)\left|sin2x\right|\) ; \(\forall x\in D\)
\(\Leftrightarrow\left(m+1\right)\left|sin2x\right|=-\left(m+1\right)\left|sin2x\right|\) ; \(\forall x\in D\)
\(\Leftrightarrow m+1=0\Leftrightarrow m=-1\)
PV
0
MH
1
TA
5 tháng 8 2021
`(m^2+m)cos2x=m^2-m-3-m^2 cos2x`
`<=> (2m^2+m)cos2x=m^2-m-3`
`<=>cos2x =(m^2-m-3)/(2m^2+m)`
PT có nghiệm `<=> -1 <= (m^2-m-3)/(2m^2+m) <=1`
`<=> [(m<=-1 \vee m>=1),(-1/2 < m <0):}`
???????????????????????????????????
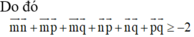
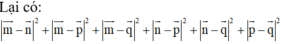
???????? hỏi thế ai mà trả lời đc