Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A sai, vì nếu x= 3 thì x2-4x+3=0
\(\overline{A}:\exists x\in R,x^2-4x+3=0\) (đúng)

C: “∀ x ∈ R : x < x + 1”.
C− : “∃ x ∈ R: x ≥ x + 1”.
C− sai vì x + 1 luôn lớn hơn x.

a) Phủ định của mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} \ne 2x - 2\)” là mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} = 2x - 2\)”
Mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} = 2x - 2\)” sai vì \({x^2} \ne 2x - 2\)với mọi số thực x ( vì \({x^2} - 2x + 2 = {(x - 1)^2} + 1 > 0\) hay \({x^2} > 2x - 2\)).
b) Phủ định của mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} \le 2x - 1\)” là mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} > 2x - 1\)”
Mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} > 2x - 1\)” đúng vì có \(x = 2 \in \mathbb{R}:{2^2} > 2.2 - 1\) hay \(4 > 3\) (luôn đúng).
c) Phủ định của mệnh đề “\(\exists x \in \mathbb{R},\;x + \frac{1}{x} \ge 2\)” là mệnh đề “\(\forall x \in \mathbb{R},\;x + \frac{1}{x} < 2\)”.
Mệnh đề “\(\forall x \in \mathbb{R},\;x + \frac{1}{x} < 2\)” sai vì \(x = 2 \in \mathbb{R}\) nhưng \(x + \frac{1}{x} = 2 + \frac{1}{2} > 2\).
d) Phủ định của mệnh đề “\(\exists x \in \mathbb{R},\;{x^2} - x + 1 < 0\)” là mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} - x + 1 \ge 0\)”.
Mệnh đề “\(\forall x \in \mathbb{R},\;{x^2} - x + 1 \ge 0\)” đúng vì \({x^2} - x + 1 = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} \ge 0\) với mọi số thực x.

+) Mệnh đề phủ định của mệnh đề A là \(\overline A \): “Đồ thị hàm số y = x không là một đường thẳng”
Mệnh đề \(\overline A \) sai vì đồ thị hàm số y = x là một đường thẳng.
+) Mệnh đề phủ định của mệnh đề B là \(\overline B \): “Đồ thị hàm số \(y = {x^2}\) đi qua điểm A (3; 9)”
Mệnh đề \(\overline B \) đúng vì \(9 = {3^2}\) nên A (3;9) thuộc đồ thị hàm số \(y = {x^2}\).

D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với 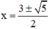
D− thỏa mãn:
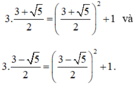
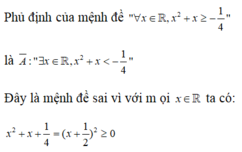
Phủ định:
\(\overline{A}="\forall x\in R;x^2-6x+9>0"\)
Mệnh đề phủ định là mệnh đề sai
Phản ví dụ: \(x=3\) thì \(x^2-6x+9=0\)