
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

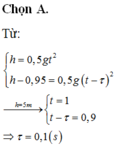

: Giọt nước thứ 2 rơi được 2 giây rồi nhỉ, vậy nên nó đi được 20m rồi 20 + 25 là được 45m nhỉ, vậy là giọt nước thì nhất đã rơi được 45m.
----- Lại áp cái công thức quen thuộc h = h0 + v0*t + 1/2 *gt^2 = 45 <=>
--------------------------------------... 5t^2 = 45 ( vì h0 tức là độ cao ban đầu bằng 0 do ta coi gốc tọa độ là nơi bắt đầu thả vật mà, v0 cũng bằng 0 luôn nhá )
--------------------------------------... => t =3s
Kết luận : Giọt nước thứ 2 rơi trễ 1s so với giọt thứ nhất.
- Với câu 1 thì chắc chúa mới trả lời được vì đâu có cho khoảng cách giữa 2 tầng tháp. VD nếu là 5m thì gặp nhau ngay lúc thả vật 2, nhỏ hơn 5m thì nó không bao giờ gặp cho đến khi nằm yên ở mặt đất, trên 5m thì mới phải tính toán.
- Với câu 2 : Giọt nước thứ 2 rơi được 2 giây rồi nhỉ, vậy nên nó đi được 20m rồi 20 + 25 là được 45m nhỉ, vậy là giọt nước thì nhất đã rơi được 45m.
----- Lại áp cái công thức quen thuộc h = h0 + v0*t + 1/2 *gt^2 = 45 <=>
--------------------------------------... 5t^2 = 45 ( vì h0 tức là độ cao ban đầu bằng 0 do ta coi gốc tọa độ là nơi bắt đầu thả vật mà, v0 cũng bằng 0 luôn nhá )
--------------------------------------... => t =3s
Kết luận : Giọt nước thứ 2 rơi trễ 1s so với giọt thứ nhất.

Thời gian rơi của các giọt là: \(t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.16}{10}}=\frac{4\sqrt{5}}{5}s\)
Có năm giọt nước nên có bốn khoảng nên là khoảng thời gian rơi liên tiếp giữa các giọt là: \(\Delta t=\frac{t}{4}=\frac{\frac{4\sqrt{5}}{5}}{4}=\frac{\sqrt{5}}{5}s\)
Quãng đường giọt ba và giọt bốn lần lượt rơi được là: \(s_3=\frac{1}{2}.g.\left(2\Delta t\right)^2=\frac{1}{2}.10.\left(2.\frac{\sqrt{5}}{2}\right)^2=4m\)
\(s_4=\frac{1}{2}.g.\left(\Delta t\right)^2=\frac{1}{2}.10.\left(\frac{\sqrt{5}}{2}\right)^2=1m\)
Vậy khoảng cách giữa giọt thứ ba và giọt thứ bốn bằng: \(s_{34}=s_3-s_4=4-1=3m\)