Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


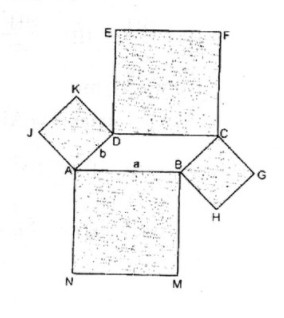
Hình đa giác đó gồm hình bình hành ABCD, hình vuông ABMN, BHGC, CFED, DKJA.
\(S_{ABMN}=S_{CDEF}=a^2\)
\(S_{BHGC}=S_{DKJA}=b^2\)

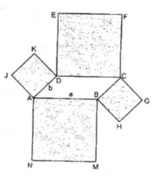
Hình đa giác đó gồm hình bình hành ABCD, hình vuông ABMN, BHGC, CFED, DKJA.
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2
Diện tích đa giác bằng :
S A B M N = S C D E F = a 2
S B H G C = S D K J A = b 2

có tam giác ABD=BCD (c.c.c) suy ra CK=AH
xét tứ giác AKCH có ck=ah cmt hkc=ahk=90 độ ( so le trong )
-> ah//kc -> AKCH là hình bình hành (dhnb)
-> CH=AK xét tam giác ADK và BCH có BC=AD CH=AK cmt có góc ADH= góc CBK so le trong
-> ADK=BCH (c.g.c) xét tam giác ABH VÀ CKH = nhau (c.g.c)-> diện tích=nhau
( chứng minh tượng tự ) - Ta có đa giác ABCH = AHB+CHD
và ADCK=AKD+CKD MÀ AHB=Ckd cmt . ADK = BCH cmt
-> tứ giác ABCH=ADCK
A D B C H K 1 2 2 1
Xét 2 tam giác vuông HDA và KBC có :
AD = BC ( ABCD - hbh )
\(\widehat{D1}=\widehat{B1}\)( so le trong , AD // Bc )
\(\Rightarrow\)\(\Delta HDA=\Delta KBC\)( ch-gn )
\(\Rightarrow\)Diện tích tam giác HDA = diện tích tam giác KBC ( 1 )
Xét t/g HDC và t/g KBA :
CD = AB ( gt )
\(\widehat{D2}=\widehat{B2}\)( so le trong , CD // AB )
HD = KB ( t/g HDA = t/g KBC )
\(\Rightarrow\)\(\Delta HDC=\Delta KBA\)( c-g-c )
\(\Rightarrow\)Diện tích tam giác HDC = diện tích tam giác KBA ( 2 )
Diện tích ABCH = diện tích KBA + diện tích AK Ch + diện tích KBC ( 3 )
Diện tích ADCK = diện tích HDC + diện tích AKCH + diện tích HDA ( 4 )
Từ ( 1 ) ; ( 2 ) ; ( 3 ) : ( 4 ) suy ra diện tích đa giác ABCH = diện tích ADCK ( đpcm )

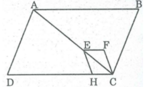
Ta có:
△ ABC = △ CDA (c.c.c) ⇒ S A B C = S C D A (1)
△ EFC = △ CHE (c.c.c) ⇒ S E F C = S C H E (2)
Từ (1) và (2) ⇒ S A B C - S E F C = S C D A - S C H E
Hay S A B C F E = S A E H D