Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



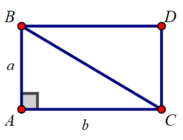
Muốn tính diện tích tam giác vuông ABC, ta dựng hình chữ nhật ABDC như trên
- ∆ABC = ∆DCB (hai cạnh góc vuông)
⇒SABC = SDCB (theo tính chất 1 diện tích đa giác) (1)
Đường chéo BC chia hình chữ nhật ABDC thành 2 phần là ∆ABC và ∆DCB
⇒SABDC = SABC + SDCB (theo tính chất 2 diện tích đa giác) (2)
Từ (1) và (2) ⇒ SABDC = 2SABC ⇒ SABC = 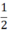 SABDC
SABDC
- ABDC là hình chữ nhật ⇒ SABDC = a.b
⇒ SABC = 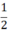 SABDC =
SABDC = 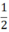 ab
ab

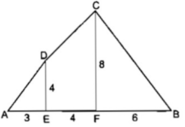
Chia đa giác ABCD thành tam giác vuông AED, hình thang vuông EDCF và tam giác vuông FCB.
S A E D = 1/2 AE.DE = 1/2. 3. 4 = 6( c m 2 )
S E D C F = (ED + FC)/2. EF = (4 + 8)/2. 4 = 24 ( c m 2 )
S C F B = 1/2 CF. FB = 1/2 .8 .6 = 24 ( c m 2 )
S A B C D = S A E D + S E D C F + S C F B = 6 + 24 + 24 = 54 ( c m 2 )

Bài giải:
SADEF=\(\dfrac{\left(AD+EF\right).FG}{2}=\dfrac{\left(4+2\right).2}{2}=6\left(cm^2\right)\)
SABCD=\(\dfrac{\left(AD+BC\right).BG}{2}=\dfrac{\left(4+1\right).1}{2}=2,5\left(cm^2\right)\)
=> SABCDEF= SADEF+SABCD= 6+2,5=8,5(cm2)
b) SDEA=\(\dfrac{DE.AE}{2}=\dfrac{4.3}{2}=6\left(cm^2\right)\)
SDCFE=\(\dfrac{\left(DE+CF\right).EF}{2}=\dfrac{\left(4+8\right).4}{2}=24\left(cm^2\right)\)
SCFB=\(\dfrac{CF.FB}{2}=\dfrac{8.6}{2}=24\left(cm^2\right)\)
=> SABCD=SDEA+SDCFE+SCFB=6+24+24=54(cm2)

a) Gọi số cạnh của đa giác đều là n
Một góc trong của đa giác đều n-cạnh có số đo là

Tổng số đo các góc ngoài của đa giác đều n-cạnh là 360o
Ta có:
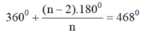
=> n(360o + 180o - 468o) = 360o
<=> n.72o = 360o
<=> n = 5
Vậy đa giác đều có 5 cạnh.
b) Ta có: AB2 + AC2 = BC2 (Py-ta-go)
<=> 62 + AC2 = 102
=> AC2 = 64 => AC = 8 (cm)
Diện tích tam giác ABC là: (6.8)/2 = 24 (cm2)