Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

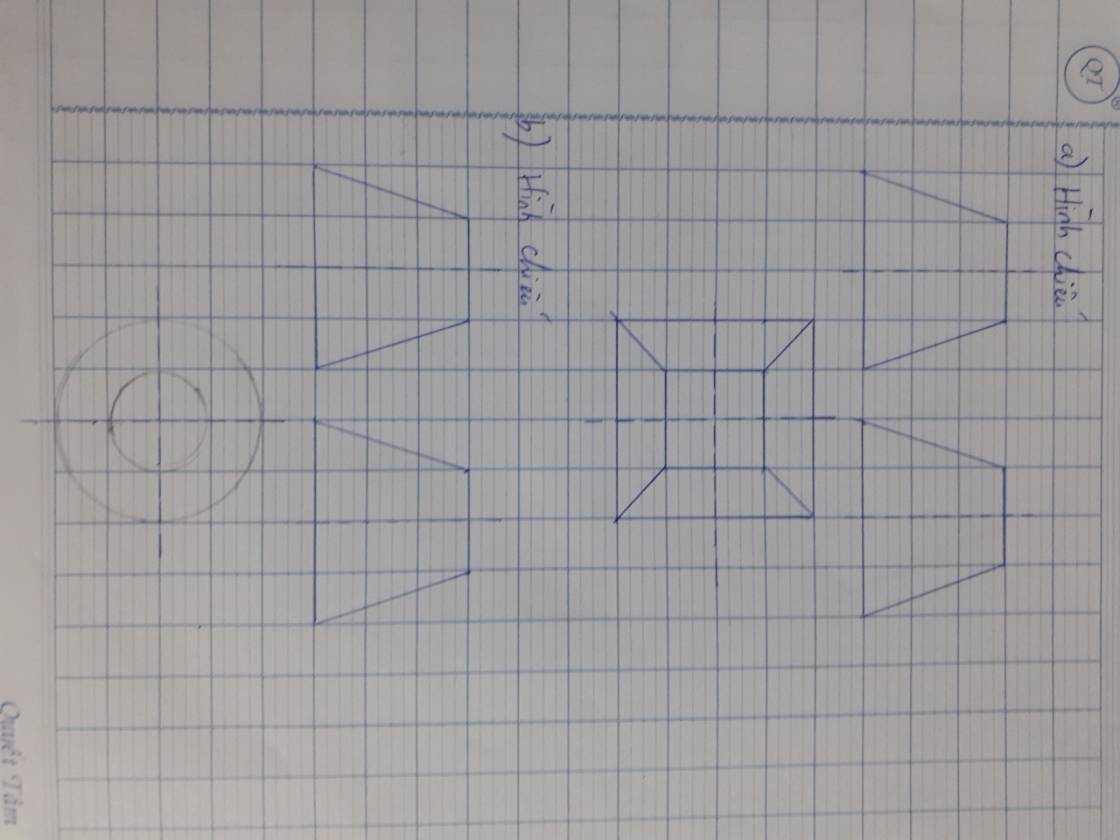
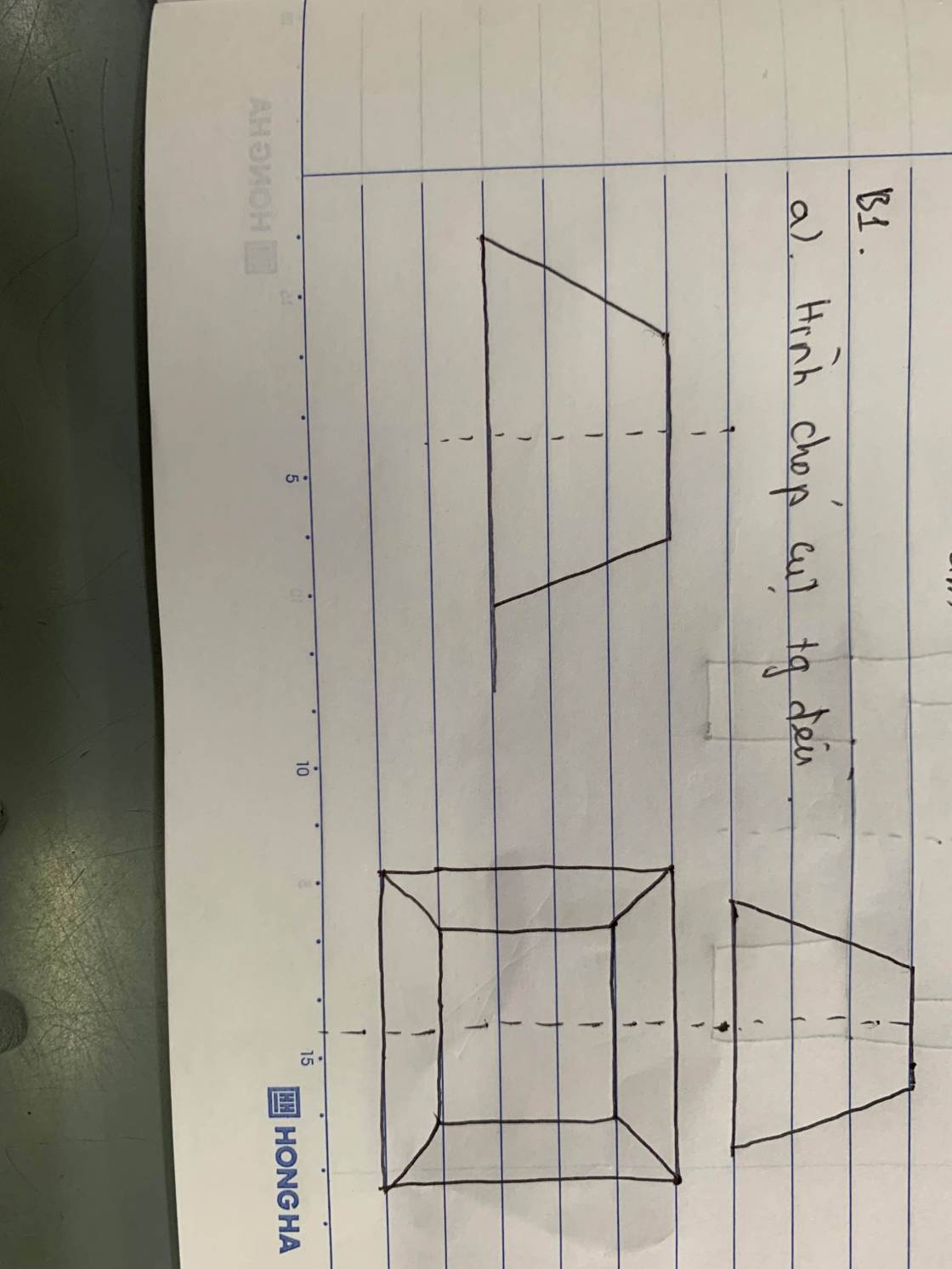
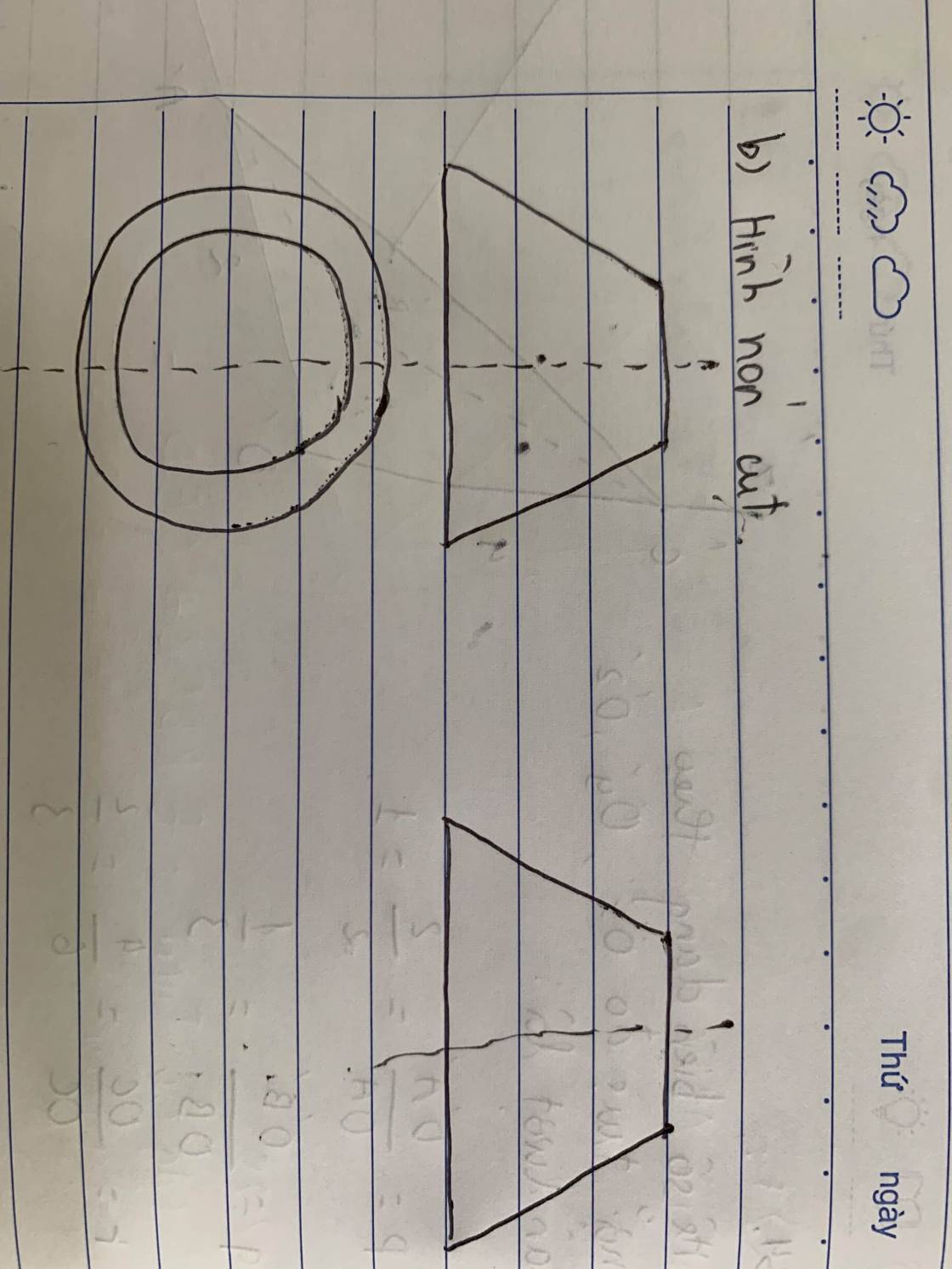
a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
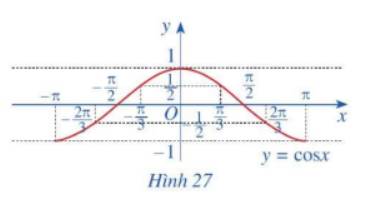
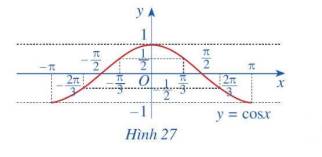
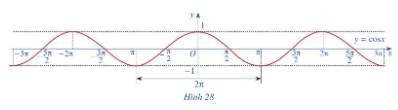
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
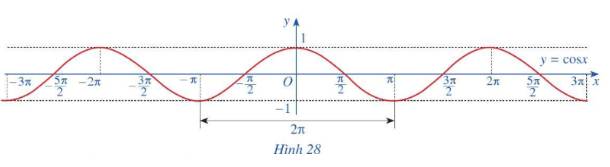
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

Tham khảo:
Mẫu a, b là mẫu số liệu ghép nhóm.
a)

- Có 5 sinh viên chi dưới 50 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 12 sinh viên chi từ 50 đến dưới 100 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 23 sinh viên chi từ 100 đến dưới 150 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 17 sinh viên chi từ 150 đến dưới 200 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
- Có 3 sinh viên chi từ 200 đến dưới 250 nghìn đồng cho việc thanh toán cước điện thoại trong tháng.
Như vậy, đa số sinh viên chi từ 100 đến dưới 150 nghìn đồng mỗi tháng cho cước điện thoại và có ít sinh viên chi trên 200 nghìn đồng cho cước điện thoại mỗi tháng.
b)

- Có 7 ngày có nhiệt độ từ đến dưới.
- Có 15 ngày có nhiệt độ từ đến dưới.
- Có 12 ngày có nhiệt độ từ đến dưới.
- Có 6 ngày có nhiệt độ từ đến dưới.

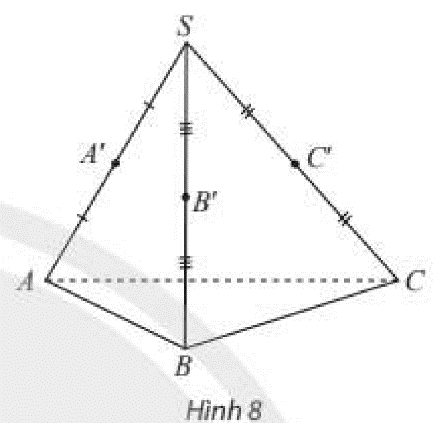
\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {ABC} \right)\\B \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AB \subset \left( {ABC} \right)\\\left. \begin{array}{l}B \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow BC \subset \left( {ABC} \right)\\\left. \begin{array}{l}A \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AC \subset \left( {ABC} \right)\end{array}\)
\(SA \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow SA\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SB \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow SB\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SC \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow SC\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow A'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow A'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow B'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow B'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow C'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow C'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(B'\) là trung điểm của \(SB\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow B'C'\) là đường trung bình của tam giác \(SBC\)
\(\left. \begin{array}{l} \Rightarrow B'C'\parallel BC\\BC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow B'C'\parallel \left( {ABC} \right)\)

Trong Hình 4b, góc lượng giác là (Oz,Ot) với tia đầu là tia Oz và tia cuối là tia Ot

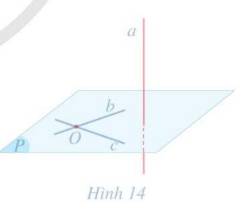
a) Ta có: a // a’ mà a’ ⊂ (Q) nên a // (Q);
b // b’ mà b’ ⊂ (Q) nên b // (Q).
Do a // (Q);
b // (Q);
a, b cắt nhau tại M và cùng nằm trong mặt phẳng (P)
Suy ra (P) // (Q).
b) Do (R) // (Q) nên trong mp(R) tồn tại hai đường thẳng a’’, b’’ đi qua M và lần lượt song song với a’, b’ trong mp(Q).
Ta có: a // a’, a’’ // a’ nên a // a’’.
Mà a’’ ∈ (R), do đó a // (R)
Do hai mặt phẳng (P) và (R) có một điểm chung nên chúng có đường thẳng chung d.
Ta có: a // (R);
a ⊂ (P);
(P) ∩ (R) = d.
Suy ra a // d.
Mà a, d cùng nằm trong mặt phẳng (P) và cùng đi qua điểm M nên đường thẳng a chính là giao tuyến của hai mặt phẳng (P) và (R).
Chứng minh tương tự ta cũng có đường thằng b cũng là giao tuyến của hai mặt phẳng (P) và (R).
Như vậy, hai mặt phẳng (P) và (R) có hai giao tuyến a và b nên (P) và (R) là hai mặt phẳng trùng nhau.








Các đường thẳng nằm trong mặt phẳng sàn nhà là: mép chân giường, chân tường, mép chân bàn, viền thảm trải sàn,…
Các đường thẳng song song với mặt phẳng sàn nhà là: mép cạnh bàn, mép kệ, mép trần nhà, mép cửa sổ,…
Các đường thẳng cắt mặt phẳng sàn nhà là: cạnh tường, cạnh thẳng đứng của kệ, tủ,…