Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
là VTCP của 2 đường thẳng d và d’. Nếu 
thì:
. Khi đó 
bằng:
. Tính 
. Khi đó:
.
. Tìm b.
.
. Tính 
.
và 
. Khi đó:
.
với 
.
và 
. Khi đó 
bằng:
. Khi đó 
bằng:
. Khi đó 
bằng
. Tính 
.
2 : cho ab=cd(a,b,c,d≠0)ab=cd(a,b,c,d≠0) và đôi 1 khác nhau, khác đôi nhau
Chứng minh :
a) C1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{{}\begin{matrix}a=kb\\c=kd\end{matrix}\right.\)
\(\frac{a-b}{a+b}=\frac{kb-b}{kb+b}=\frac{b\left(k-1\right)}{b\left(k+1\right)}=\frac{k-1}{k+1}\)
\(\frac{c-d}{c+d}=\frac{kd-d}{kd+d}=\frac{d\left(k-1\right)}{d\left(k+1\right)}\frac{k-1}{k+1}\)
Bài 1:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{\dfrac{3}{2}}=\dfrac{z}{\dfrac{4}{3}}=\dfrac{x-y}{2-\dfrac{3}{2}}=\dfrac{15}{\dfrac{1}{2}}=30\)
Do đó: x=60; y=45; z=40
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
Do đó: x=20; y=30; z=42
xAB + ABE
= 400 + 1400
= 1800
=> xAB và ABE là 2 góc bù nhau
mà 2 góc này ở vị trí trong cùng phía
=> Ax // DE
=> xAB = DBA
mà xAB = 400 (gt)
=> DBA = 400
BCy + CBD = 1800 (2 góc trong cùng phía, DE // Cy)
1300 + CBD = 1800
CBD = 1800 - 1300
CBD = 500
mà DBA = 400 (chứng minh trên)
=> CBD + DBA = 500 + 400 = 900
=> ABC = 900
=> AB _I_ BC
xAB + ABE
= 400 + 1400
= 1800
=> xAB và ABE là 2 góc bù nhau
mà 2 góc này ở vị trí trong cùng phía
=> Ax // DE
=> xAB = DBA
mà xAB = 400 (gt)
=> DBA = 400
BCy + CBD = 1800 (2 góc trong cùng phía, DE // Cy)
1300 + CBD = 1800
CBD = 1800 - 1300
CBD = 500
mà DBA = 400 (chứng minh trên)
=> CBD + DBA = 500 + 400 = 900
=> ABC = 900
=> AB _I_ BC
\(sin^4\left(x+\dfrac{\pi}{2}\right)-sin^4x=sin4x\)
\(\Rightarrow cos^4x-sin^4x=sin4x\)
\(\Rightarrow\left(cos^2x+sin^2x\right)\left(cos^2x-sin^2x\right)=sin4x\)
\(\Rightarrow cos^2x-sin^2x=4sinx.cosx.cos2x\)
......
Ta nhận xét rằng khi thả bóng thì bóng đi được 1 lược còn kể từ lần nảy đầu tiên đến khi dừng lại thì bóng đi được 2 lược (1 nảy lên và 1 rơi xuống). Giả sử sau lần nảy thứ n + 1 thì bóng dừng hẳn.
Quãng đường bóng đi được tính đến lần chạm sàn thứ nhất là:
\(S_1=63\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ 2 là:
\(S_2=63+63.\dfrac{1^1}{10^1}\)
Quãng đường bóng đi được tính đến lần chạm sàn thứ (n + 1) là:
\(S_{n+1}=63+63.\left(\dfrac{1}{10}+\dfrac{1}{10^2}+...+\dfrac{1}{10^n}\right)\)
\(=63+63.\dfrac{\dfrac{1}{10}}{1-\dfrac{1}{10}}=70\left(m\right)\)
Vậy độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất là \(70\left(m\right)\)
Đáp án B.
Gọi x (phút) là thời gian mà bạn A đến chờ ở thư viện.
Gọi y (phút) là thời gian mà bạn B đến chờ ở thư viện.
Điều kiện: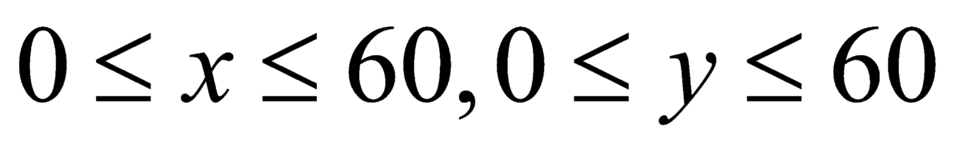
Điều kiện gặp nhau là
Do điểm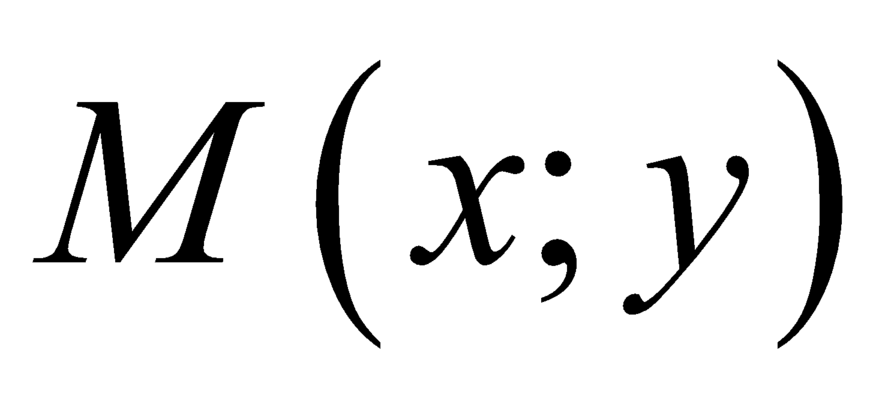
thỏa điều kiện (*) thuộc lục giác gạch sọc giới hạn bởi 2 đường thẳng 
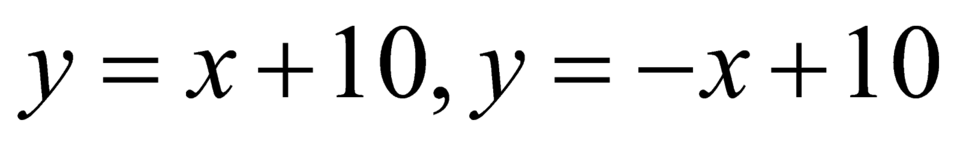là hình vuông của không gian mẫu.
Lục giác có diện tích
Vậy xác suất để 2 người gặp nhau là: