Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Độ biến dạng của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=\dfrac{1.10}{100}=0,1m=10cm\)
\(\omega=\sqrt{\dfrac{k}{m}}=10(rad/s)\)
Áp dụng CT: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2^2+\dfrac{(20\sqrt 3)^2}{10^2}\)
\(\Rightarrow A = 4cm\)
Lực đàn hồi cực đại:
\(F_{dhmax}=k\Delta\ell_{max}=k(\Delta\ell_0+A)=100.(0,1+0,04)=14(N)\)
Lực đàn hồi cực tiểu:
\(F_{dhmin}=k\Delta\ell_{min}=k(\Delta\ell_0-A)=100.(0,1-0,04)=6(N)\)

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Đáp án C
Hướng dẫn:
+ Tại vị trí cân bằng O của hệ hai vật lò xo giãn Δ l = m B + m A k = 0 , 2 + 0 , 1 50 = 6 cm
Nâng hai vật đến vị trí lò xo có chiều dài tự nhiên rồi thả nhẹ, con lắc sẽ dao động với biên độ A = 6 cm.
+ Hai vật dao động đến vị trí lực đàn hồi lớn nhất, vị trí này phải là vị trí biên dương. Sau khi B tách ra, A sẽ dao động điều hòa quanh vị trí cân bằng mới O′, vị trí này nằm trên O một đoạn O O ' = m B g k = 0 , 2.10 50 = 4 cm.
→ Biên độ dao động mới của con lắc sẽ là A = 4 + 6 = 10 cm.
Chiều dài nhỏ nhất của lò xo sẽ là l m i n = l 0 + Δ l 0 – A = 22 c m .

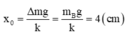
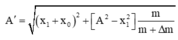


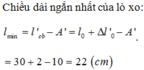
Hướng dẫn:
Nhận thấy rằng việc vật B tách ra khỏi vật A làm thay đổi vị trí cân bằng và cả tần số góc dao động của con lắc lúc sau.
Để đơn giản, ta có thể tách chuyển động của hệ thành hai giai đoạn sau:
Giai đoạn 1: Hai vật dao động quanh vị trí cân bằng O từ biên âm đến biên dương.
+ Độ biến dạng của lò xo tại vị trí cân bằng của hai vật đúng bằng biên độ dao động:
Δ l 0 = m A + m B g k = 3 m A g k = 6 c m
+ Lực đàn hồi có độ lớn cực đại tại vị trí biên dưới.
Giai đoạn 2: Vật B tách ra khỏi vật A rơi tự do, vật A dao động điều hòa quanh vị trí cân bằng mới O′.
Vị trí cân bằng mới O′ nằm trên vị trí cân bằng cũ O một đoạn O O ' = m B g k = 0 , 2.10 50 = 4 c m
+ Tại vị trí vật B tách ra khỏi vật A ta có x′ = 6 + 4 = 10 cm, v′ = 0
→ Biên độ dao động mới A′ = x′ = 10 cm
Chiều dài ngắn nhất của lò xo lmin = 30 + 2 – 10 = 22 cm
Đáp án A