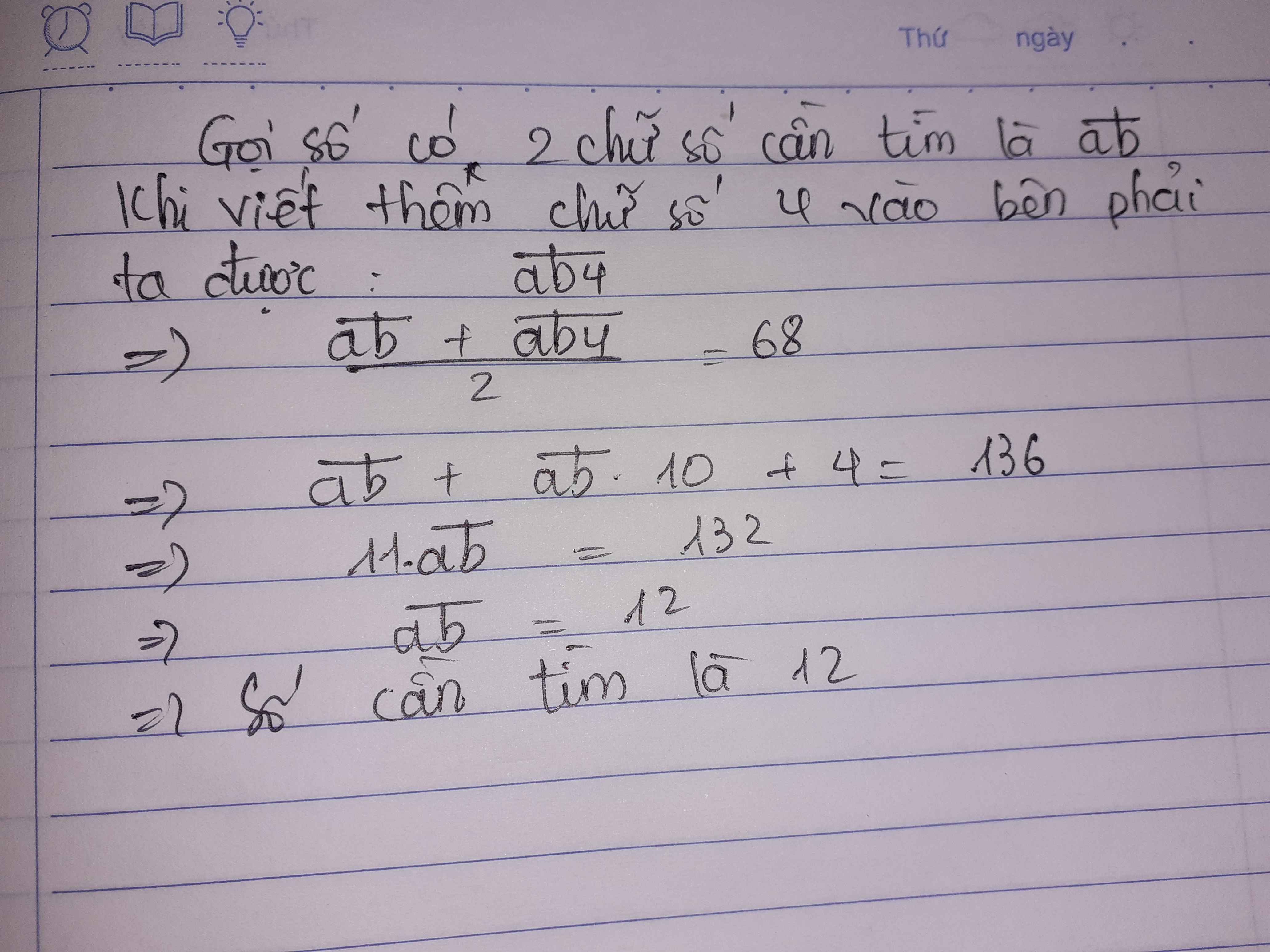Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi số cần tìm là $\overline{ab}$ với $a,b\in\mathbb{N}; a,b\leq 9; a\neq 0$
Theo bài ra ta có:
$(\overline{ab}+\overline{ab4}):2=68$
$(\overline{ab}+\overline{ab}.10+4)=136$
$11\overline{ab}+4=136$
$11\overline{ab}=132$
$\overline{ab}=12$
Vậy số cần tìm là $12$

Gọi số đó là abc, ta được:
abc3 - abc = 1803
<=> (abc0 + 3) - abc = 1803
<=> (abc x 10 + 3) - abc = 1803
<=> abc x 10 + 3 - abc = 1803
<=> abc(10 - 1) + 3 =1803
,<=> 9 x abc + 3 = 1803
=> 9 x abc =1803 - 3 = 1800
=> abc = 1800 : 9
=> abc = 200

gọi a,b lần lượt là các số mới và số cũ
Khi viết thêm chữ số đó thì hiệu của số mới và số cũ 300
để a chia hết cho b thì a phải giảm đi 10 đơn vị =>a-b=300-10=290
Khi đó a/b=11/1
=>b=290:(11-1) x 1=29
Vậy số cần tìm là 29

3ab=11.ab +10
=>300+ab=11.ab +10
=>300=10.(ab+1)
=>ab+1=30
=>ab=29