
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi giá trị của chữ số sau khi xóa đi số 5 là x (với \(x>0;x\in N\))
Giá trị chữ số ban đầu: \(10x+5\)
Theo bài ra ta có pt:
\(10x+5-x=1796\)
\(\Rightarrow9x=1791\)
\(\Rightarrow x=199\)
Vậy chữ số đó là \(1995\)

Câu 8:
\(x^2+\left(2m+1\right)x-m^2=0\)
a=1; b=2m+1; c=-m2
Vì ac<=0 nên phương trình luôn có nghiệm
Theo đề, ta có: \(A=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(2m+1\right)^2-8\left(-m^2\right)\)
\(=4m^2+4m+1+8m^2=12m^2+4m+1\)
\(=12\left(m^2+\dfrac{1}{3}m+\dfrac{1}{12}\right)\)
\(=12\left(m^2+2\cdot m\cdot\dfrac{1}{6}+\dfrac{1}{36}+\dfrac{1}{18}\right)\)
\(=12\left(m+\dfrac{1}{6}\right)^2+\dfrac{2}{3}\ge\dfrac{2}{3}\forall m\)
Dấu '=' xảy ra khi m=-1/6

\(=\dfrac{\sqrt{x}+2-\sqrt{x}}{x-4}\cdot\dfrac{x+2}{1}=\dfrac{2\left(x+2\right)}{x-4}=\dfrac{2x+4}{x-4}\)


Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét (B;BA) có
BA là bán kính
CA vuông góc BA tại A
Do đó: CA là tiếp tuyến của (B;BA)

Xét ΔABC có
BE,CF là đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếpΔABC
=>d(I;BC)=d(I;AB)=d(I;AC) và AI là phân giác của góc BAC
ΔABC cân tại A
mà AI là phân giác
nên AI vuông góc BC tại D
=>d(I;BC)=ID
=>d(I;AB)=d(I;AC)=ID
=>AB,AC là tiếp tuyến của (I;ID)

Bài 2:
a: Xét (O) có
CM,CA là tiếp tuyến
Do đó: CM=CA và OC là phân giác của \(\widehat{AOM}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{BOM}\)
\(\widehat{AOM}+\widehat{BOM}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
b: CD=CM+MD
mà CM=CA và DM=DB
nên CD=CA+DB
c: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=OM^2=R^2\) không đổi

a: T=20*5000-500=99500(ngàn đồng)
b: T=9000*8=72000
Số sản phẩm bán được sẽ thỏa mãn:
20n-500=72000
=>n-25=3600
=>n=3625
 giúp e với ạaa
giúp e với ạaa

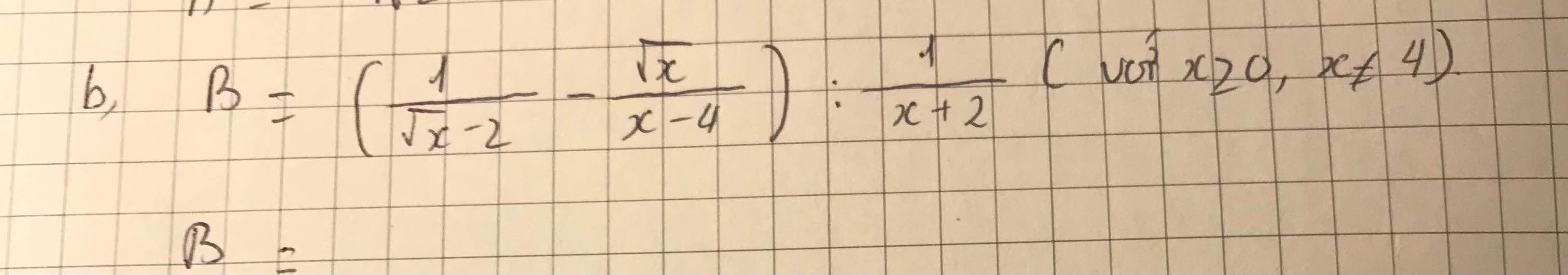
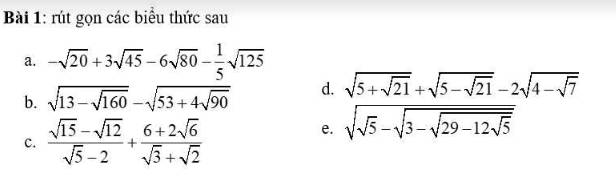 giúp e với ạaa
giúp e với ạaa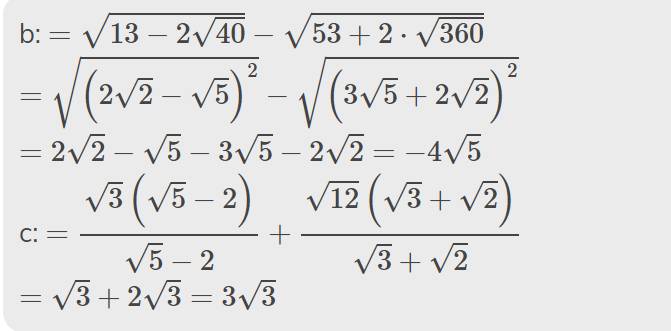
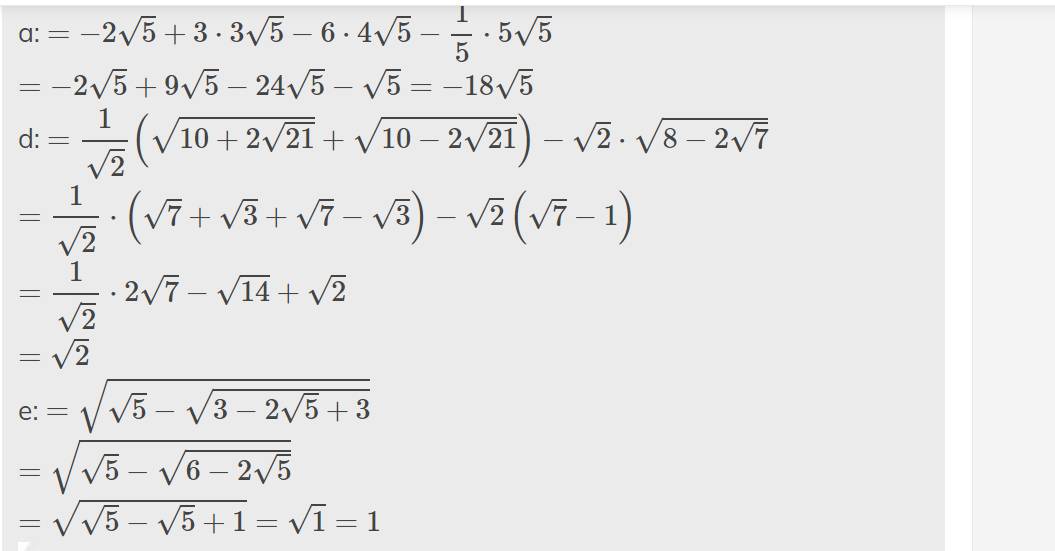

 giúp e gấp với ạaa
giúp e gấp với ạaa giúp e gấp với ạaa
giúp e gấp với ạaa
