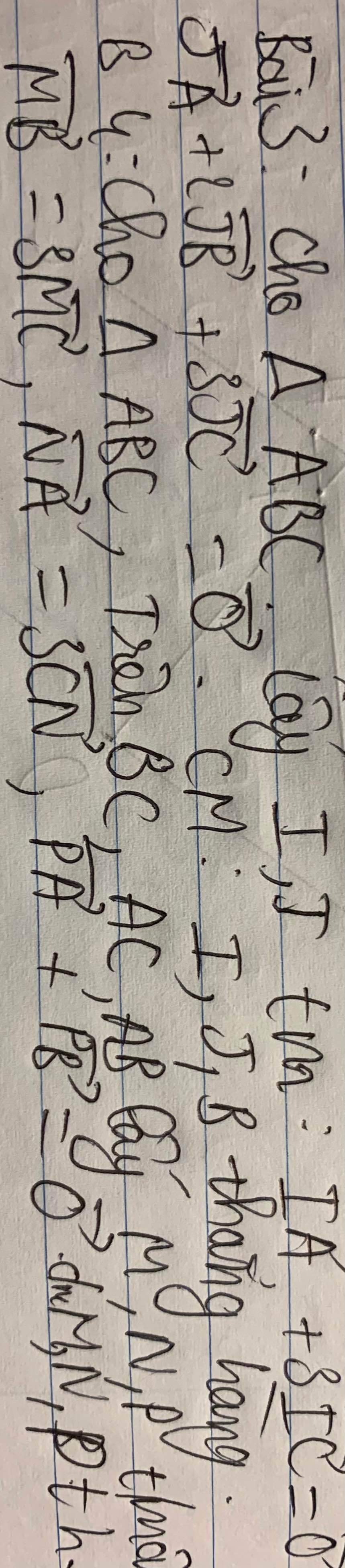K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
E
4
26 tháng 8 2019
mik 2k7 nhung co
bai j khong biet
ban se gui cho mik nhe!
mik lam cho
QD
2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
3.
\(\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{0}\Rightarrow\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{IB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{BC}=\overrightarrow{0}\Rightarrow4\overrightarrow{IB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (1)
\(\overrightarrow{JA}+2\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\Rightarrow\overrightarrow{JB}+\overrightarrow{BA}+2\overrightarrow{JB}+3\overrightarrow{JB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow6\overrightarrow{JB}+\overrightarrow{BA}+3\overrightarrow{BC}=0\Rightarrow6\overrightarrow{JB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (2)
(1);(2) \(\Rightarrow4\overrightarrow{IB}=6\overrightarrow{JB}\Rightarrow\overrightarrow{IB}\) và \(\overrightarrow{JB}\) cùng phương
Hay I; J; B thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
4.
\(\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}\Rightarrow\overrightarrow{PA}+\overrightarrow{PA}+\overrightarrow{AB}=0\Rightarrow\overrightarrow{PA}=-\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{NA}=3\overrightarrow{CN}\Rightarrow\overrightarrow{NA}=3\overrightarrow{CA}+3\overrightarrow{AN}\Rightarrow4\overrightarrow{AN}=3\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AN}=\dfrac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow2\overrightarrow{BM}=3\overrightarrow{BC}\Rightarrow\overrightarrow{BM}=\dfrac{3}{2}\overrightarrow{BC}=\dfrac{3}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{PN}=\overrightarrow{PA}+\overrightarrow{AN}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) (1)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=-\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=2\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)\) (2)
(1);(2) \(\Rightarrow\overrightarrow{PM}=2\overrightarrow{PN}\Rightarrow\) P, M, N thẳng hàng
KN
1
16 tháng 5 2022
a: Xét ΔBKC vuông tại K và ΔCHB vuông tại H có
BC chung
\(\widehat{KBC}=\widehat{HCB}\)
Do đó: ΔBKC=ΔCHB
Suy ra: BK=CH
b: Xét ΔAIC vuông tại I và ΔBHC vuông tại H có
góc C chung
Do đó ΔAIC\(\sim\)ΔBHC
Suy ra: CA/CB=CI/CH
hay \(CA\cdot CH=CI\cdot CB\)
c: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
TH
2
N
23 tháng 9 2016
1)Ta có:\(\sin2\alpha=2\sin\alpha.\cos\alpha\)
\(1+\cos2\alpha=2\cos^2\alpha\)
\(\Rightarrow A=\frac{2\sin\alpha.\cos\alpha+\sin\alpha}{2\cos^2\alpha+\cos\alpha}=\frac{\sin\alpha\left(2\cos\alpha+1\right)}{\cos\alpha\left(2\cos\alpha+1\right)}=\frac{\sin\alpha}{\cos\alpha}=\tan\alpha\)
