
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$


ta có : CK vuông góc DB (1)
AH vuông góc DB (2)
từ (1),(2) suy ra AH//CK (*)
xét tam giác vuông AHD và tam giác vuông CBK:ta có
góc H=góc K=90
góc ADH=góc CBK(slt)
suy ra 2 tam giác đó bằng nhau
suy ra AH=CK (*')
từ (*),(*') ta có tứ giác AHCK là hình bình hình

Đề sai nên mình sửa chút , 214 chứ không phải 2014 .
(x-214)/86 + (x-132)/84 + (x-54)/82 = 6
- (x-214)/86 + (x-132)/84 + (x-54)/82 - 6 =0
- (x-214)/86 - 1 + (x-132)/84 -2 +(x-54)/82 - 3 =0
- (x-300)/86 + (x-300)/84 +(x-300)/82 =0
- (x - 300 )(1/86 +1/84 +1/82 )=0
- x - 300=0
- x =300 vì 1/86 +1/84 +1/82 khác 0.



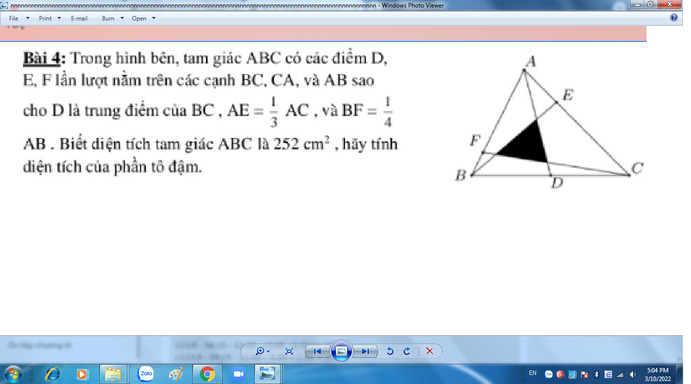
 giúp mik với nha!
giúp mik với nha!

Gọi h là độ dài chiều cao của đỉnh A ứng với cạnh BC
Ta có, diện tích tam giác ABC là: \(S_{ABC}=\dfrac{1}{2}h.BC=90\left(cm^2\right)\left(1\right)\)
Lại có, diện tích tam giác ABM là: \(S_{ABM}=\dfrac{1}{2}h.BM\left(2\right)\)
Lấy (1) chia (2) ta có: \(\dfrac{BC}{BM}=\dfrac{90}{S_{ABM}}\Leftrightarrow\dfrac{4BM}{BM}=\dfrac{90}{S_{ABM}}\Leftrightarrow4=\dfrac{90}{S_{ABM}}\Rightarrow S_{ABM}=22,5cm^2\)