
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


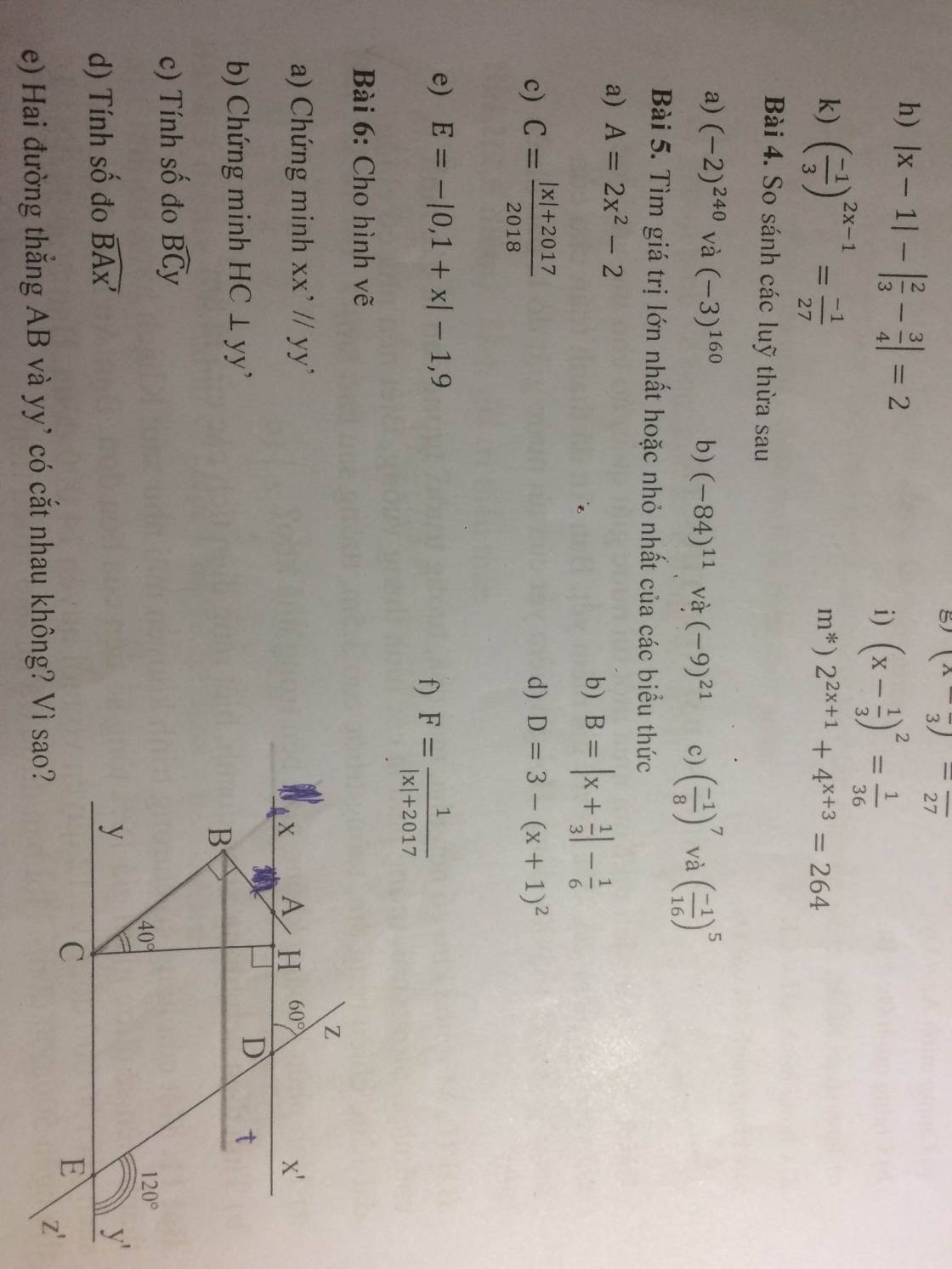
a) ∠CEz + ∠zEy' = 180⁰ (kề bù)
⇒ ∠CEz = 180⁰ - ∠zEy'
= 180⁰ - 120⁰
= 60⁰
⇒ ∠CEz = ∠xDz = 60⁰
Mà ∠CEz và ∠xDz là hai góc đồng vị
⇒ xx' // yy'
b) Do HC ⊥ xx' (gt)
xx' // yy' (cmt)
⇒ HC ⊥ yy'
c) Do HC ⊥ yy' (cmt)
⇒ ∠HCy = 90⁰
⇒ ∠BCy = ∠HCy - ∠BCH
= 90⁰ - 40⁰
= 50⁰
c) Vẽ tia Bt // xx'//yy'
⇒ ∠CBt = ∠BCy = 50⁰ (so le trong)
⇒ ∠ABt = ∠ABC - ∠CBt
= 90⁰ - 50⁰
= 40⁰
Do Bt // xx'
⇒ ∠xAB = ∠ABt = 40⁰ (so le trong)
Ta có:
∠BAx' + ∠xAB = 180⁰ (kề bù)
⇒ ∠BAx' = 180⁰ - ∠xAB
= 180⁰ - 40⁰
= 140⁰
e) Do AB cắt tia Bt tại B
Mà Bt // yy'
⇒ AB cắt yy'

Bài 2.
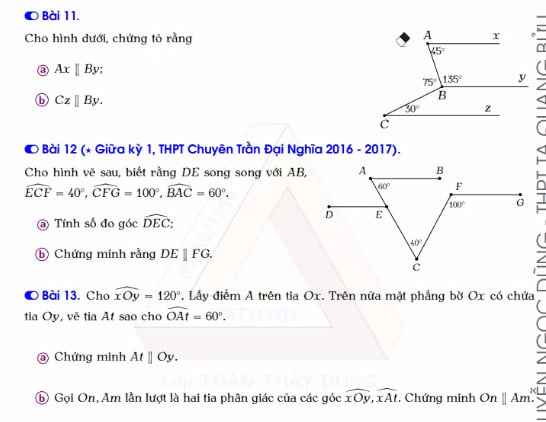
a. góc xAB + góc ABy = 45+135 = 180 (độ)
--> góc xAB và ABy là hai góc trong cùng phía bù nhau
--> Ax // By (đpcm)
b. góc CBy =360 - 75 -135 = 150 (độ)
--> góc CBy + góc CBz = 150 +30 =180 (độ)
--> góc CBy và CBz là hai góc trong cùng phía bù nhau
--> By//Cz (đpcm)


ý bạn là \(x-y-z=-33?\)
Ta có \(2x=3y=5z\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x-y-z}{15-10-6}=\dfrac{-33}{-1}=33\\ \Rightarrow\left\{{}\begin{matrix}x=33\cdot15=495\\y=33\cdot10=330\\z=33\cdot6=198\end{matrix}\right.\)

Bạn nên cung cấp cả đề vào post để tiện cho mọi người hỗ trợ hơn bạn nhé.

a: 26⋅33=(22⋅3)3=12326⋅33=(22⋅3)3=123
b: 64⋅83=24⋅34⋅29=213⋅3464⋅83=24⋅34⋅29=213⋅34
c: 16⋅81=36216⋅81=362
d: 254⋅28=1004

Ta có : \(A\left(x\right)=x^2+4x+10=\left(x^2+4x+10\right)\)
\(=\left(x^2+2x+2x+4\right)+6\)
\(=\left(x+2\right)^2+6>0\)
Do đó \(A\left(x\right)\) không có nghiệm

bài gì ạ