Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phép thử T được xét là: "Gieo một con súc sắc hai lần".
a) Các phần tử của không gian mẫu của phép thử T được liệt kê trong bảng sau đây.
Trong bảng này, cột I là các mặt i chấm có thể xảy ra ở lần gieo thứ nhất, i =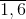 
.
Dòng II (dòng trên cùng) là các mặt j chấm có thể xảy ra ở lần gieo thứ 2, j = 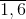. Mỗi ô (i, j) (giao của dòng i và cột j, 1 ≤ i, j ≤ 6) biểu thị một kết quả có thể có của phép thử T là: lần gieo thứ nhất ra mặt i chấm, lần gieo thứ 2 ra mặt j chấm.
Không gian mẫu:
Ta có thể mô tả không gian mẫu dưới dạng như sau:
Ω = {(i, j) 
i, j = 1, 2, 3, 4, 5, 6},
ở đó (i, j) là kết quả: " Lần đầu xuất hiện mặt i chấm, lần sau xuất hiện mặt j chấm".
Không gian mẫu có 36 phần tử.
b) A = "Lần gieo đầu được mặt 6 chấm";
B = "Tổng số chấm trong hai lần gieo là 8";
C = "Kết quả ở hai lần gieo là như nhau".
Bài 2:
a: \(=\dfrac{7}{9}\left(\dfrac{7}{6}-\dfrac{19}{20}-\dfrac{1}{15}\right)+\dfrac{22}{5}\cdot\dfrac{1}{24}\)
\(=\dfrac{7}{9}\cdot\dfrac{3}{20}+\dfrac{22}{120}=\dfrac{7}{60}+\dfrac{11}{60}=\dfrac{18}{60}=\dfrac{3}{10}\)
b: \(=\left(\dfrac{35-32}{60}\right)^2+\dfrac{4}{5}\cdot\dfrac{70-45}{80}\)
\(=\dfrac{1}{400}+\dfrac{4\cdot25}{400}=\dfrac{101}{400}\)
dài quá nên mk chỉ hướng dẫn thôi nhé .
1) +) ta có : \(y=24sinx.cosx-5\left(cos^2x-sin^2x\right)-3\)
\(\Rightarrow y\le14sin^2x+4cos^2x=10sin^2x+4\)
dấu "=" khi \(sinx=cosx=\pm\dfrac{\sqrt{2}}{2}\) \(\Rightarrow...\)
\(\Rightarrow y_{max}=9\) khi ...
ta có : \(y=12\left(sinx+cosx\right)^2-10-10cos^2x\ge-10-10cos^2x\)
dâu "=" xảy ra khi \(sinx=cosx\) \(\Rightarrow\) ...
vậy ...
2) ta có : \(y=2sin2x-1\Rightarrow-3\le y\le1\)
dấu "=" bênh phải khi \(sin2x=-1\Rightarrow...\)
dâu "=" bênh trái khi \(sin2x=1\Rightarrow...\)
mấy câu còn lại bn làm tương tự nha .
a/ \(=lim\frac{\left(-\frac{2}{3}\right)^n+1}{-2.\left(-\frac{2}{3}\right)^n+3}=\frac{1}{3}\)
b/ \(=lim\frac{\left(2-\frac{1}{n}\right)\left(1+\frac{1}{n}\right)\left(3+\frac{4}{n}\right)}{\left(\frac{5}{n}-6\right)^3}=\frac{2.1.3}{\left(-6\right)^3}=-\frac{1}{36}\)
c/ \(=lim\frac{5n+3}{\sqrt{n^2+5n+1}+\sqrt{n^2-2}}=\frac{5+\frac{3}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{2}{n}}}=\frac{5}{1+1}=\frac{5}{2}\)
d/ \(=lim\frac{5.\left(\frac{1}{2}\right)^n-6}{4.\left(\frac{1}{3}\right)^n+1}=\frac{-6}{1}=-6\)
e/ \(=-n^3\left(2+\frac{3}{n}-\frac{5}{n^2}+\frac{2020}{n^3}\right)=-\infty.2=-\infty\)
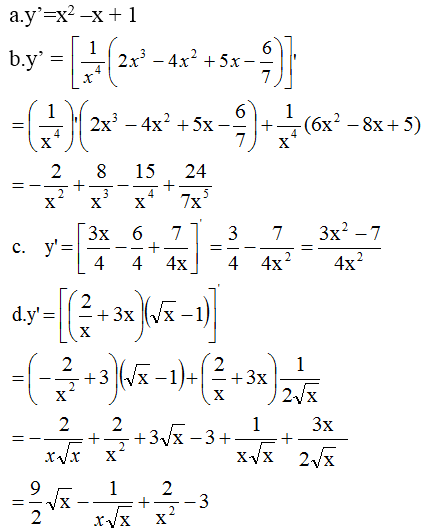
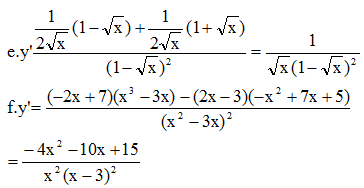
a. Không gian mẫu gồm 36 phần tử:
Ω = {(i, j) | i, j = 1, 2, 3, 4, 5, 6 }
Trong đó (i, j) là kết quả "lần đầu xuất hiện mặt i chấm, lần sau xuất hiện mặt j chấm".
b. Phát biểu các biến cố dưới dạng mệnh đề:
A = {(6,1), (6,2), (6,3), (6,4), (6, 5), (6, 6)}
- Đây là biến cố "lần đầu xuất hiện mặt 6 chấm khi gieo con súc sắc".
B = {(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)}
- Đây là biến cố " cả hai lần gieo có tổng số chấm bằng 8".
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
- Đây là biến cố " kết quả của hai lần gieo là như nhau".