
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\widehat{B}=90^0-30^0=60^0\)
XétΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
nên AB=5cm
=>\(AC=5\sqrt{3}\left(cm\right)\)
b: \(\widehat{C}=90^0-30^0=60^0\)
Xét ΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
hay \(BC=16\sqrt{3}\left(cm\right)\)
=>\(AC=8\sqrt{3}\left(cm\right)\)

- Giả sử tam giác ABC vuông tại A . Theo bài ra , ta có :
\(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\left(1\right)\)
- Áp dụng đlí Py - ta - go cho tam giác vuông ABC ( \(\widehat{A}=90^o\))
Ta có : \(BC^2=AB^2+AC^2\)
\(\Leftrightarrow125^2=\left(\frac{3}{4}AC\right)^2+AC^2\)
\(\Leftrightarrow15625=\frac{9}{16}AC^2+AC^2\)
\(\Leftrightarrow15625=\left(\frac{9}{16}+1\right)AC^2\)
\(\Leftrightarrow\frac{25}{16}AC^2=15625\)
\(\Leftrightarrow AC^2=\frac{15625.16}{25}\)
\(\Leftrightarrow AC=\sqrt{\frac{15625.16}{25}}=\frac{125.4}{5}=100\left(cm\right)\)
Thay AC = 100cm vào (1) , ta được :
\(AB=\frac{3}{4}.100=75\left(cm\right)\)
- Áp dụng hệ thức lượng trong tam giác ABC ( \(\widehat{A}=90^o\)) đường cao AH , ta có :
\(AB^2=BH.BC\)
\(\Leftrightarrow BH=\frac{AB^2}{BC}=\frac{75^2}{125}=45\left(cm\right)\)
Ta lại có : BC = BH + HC
125 = 45 + HC
HC = 125 - 45 = 80 ( cm )
Vậy : AB = 75 cm
AC = 100 cm
HC = 80 cm
BH = 45 cm


a) Ta có: \(\widehat{B}+\widehat{C}=90^o\Rightarrow\widehat{B}=90^o-\widehat{C}=90^o-30^o=60^o\)
Mà: \(sinB=sin60^o=\dfrac{AC}{BC}\Rightarrow AC=sin60^o\cdot BC=\dfrac{\sqrt{3}}{2}\cdot8=4\sqrt{3}\left(cm\right)\)
Áp dụng định lý Py-ta-go ta có:
\(AB=\sqrt{BC^2-AC^2}=\sqrt{8^2-\left(4\sqrt{3}\right)^2}=4\left(cm\right)\)
b) Ta có:
\(cosB=cos60^o=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{cos60^o}=\dfrac{10}{cos60^o}=\dfrac{10}{\dfrac{1}{2}}=20\left(cm\right)\)
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)



a: \(\widehat{B}=60^0\)
AB=8cm
\(AC=4\sqrt{3}\left(cm\right)\)

Kẻ đường cao AH ứng với BC
Đặt \(AB=x\) với \(0< x< 12\Rightarrow AC=12-x\)
Đặt \(BH=y\Rightarrow CH=8-y\) (với \(0< y< 8\))
Trong tam giác vuông ABH ta có:
\(cosB=\dfrac{BH}{AB}\Rightarrow BH=AB.cosB=\dfrac{x}{2}\Rightarrow y=\dfrac{x}{2}\)
\(\Rightarrow CH=8-y=8-\dfrac{x}{2}\)
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB=\dfrac{x\sqrt{3}}{2}\)
Áp dụng Pitago cho tam giác vuông ACH:
\(AC^2=AH^2+CH^2\Leftrightarrow\left(12-x\right)^2=\left(\dfrac{x\sqrt{3}}{2}\right)^2+\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\Rightarrow x=5\)
\(\Rightarrow AC=12-x=7\)
Vậy \(AB=5cm,AC=7cm\)

Cho tam giác ABC có BC = 8cm , góc ABC = 40 độ và ACB = 30 độ .Kẻ đường cao AH. Tính AH?
Ta có AH=BH.tan ABC=CH.tan ACB
<=>BH.tan 40=CH.tan 30
<=>BH/tan 30=CH/tan 40
<=>BH+CH/tan 30 + tan 40=8/1,4164499
<=>BH/tan 30=8/1,4164499 =>BH=3,26(cm)
==>AH=BH.tan 40=2,74(cm)
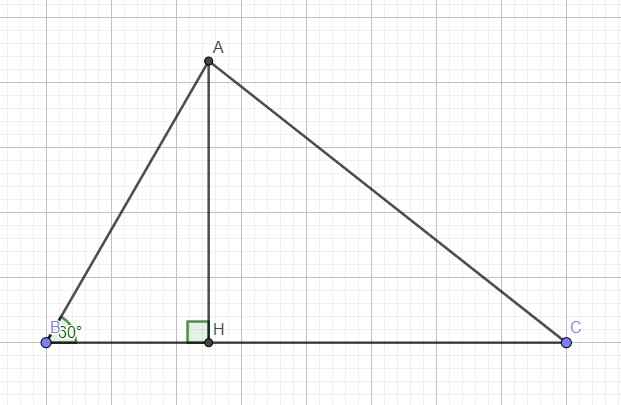
A B C H 30 40 8 cm
Xét trong tam giác vuông ABH có: \(\tan30^0.BH=AH\)
Xét trong tam giác vuông AHC có: \(\tan40^0.HC=AH\)
\(\Rightarrow\tan30^0.BH=\tan40^0.HC\)
\(\Rightarrow\frac{\sqrt{3}}{3}.BH=0,839.HC\)
\(\Rightarrow\frac{\frac{\sqrt{3}}{3}}{0,839}=\frac{HC}{BH}\Rightarrow\frac{HC}{BH}=0,688\)
\(\Rightarrow HC=0,688.BH\)
\(\Rightarrow HC+BH=0,688.BH+BH=1,688.BH=BC=8\Rightarrow BH\simeq4,739\) (cm)
\(HC=0,688.BH=0,688.4,739\simeq3,260\) (cm)
Trong tam giác ABC vuông tại A có:
\(AB^2=BH.BC\Rightarrow AB^2\simeq4,739.8\simeq37,912\Rightarrow AB\simeq6,157\) (cm)
\(AC^2=HC.BC\Rightarrow AC^2\simeq3,260.8\simeq26,083\Rightarrow AC\simeq5,107\) (cm)
Vậy .....
P/s: Đã thử lại và đúng.