
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với x≠±1x≠±1, chia hai vế của phương trình cho 4√x2−1x2−14, ta được:
34√x−1x+1+m4√x+1x−1=23x−1x+14+mx+1x−14=2
Đặt t=4√x−1x+1⇒4√x+1x−1=1tt=x−1x+14⇒x+1x−14=1t (dựa vào xx để tìm tập xác giá trị của tt)
Khi đó phương trình trở thành:3t+mt=2⇔3t2−2t+m=0(1)3t+mt=2⇔3t2−2t+m=0(1)
Bài toán trở về: Tìm mm để phương trình (1)(1) có nghiệm tt thỏa mãn điều kiện.
chúc bn học tốt

Hai pt trừ cho nhau sau đó khai triển bằng dùng hằng đẳng thức được pt tích sau đó dùng phép thế.


Nhân phương trình thứ nhất với -3 rồi cộng vào phương trình thứ hai.
Lại nhân phương trình thứ nhất rồi cộng vào phương trình thứ ba thì được hệ:
(I) ⇔ (II)
⎧⎪⎨⎪⎩x+3y+2z=1−4y−7z=6−17y−13z=−8{x+3y+2z=1−4y−7z=6−17y−13z=−8
Nhân phương trình thứ hai của hệ (II) với 17 rồi cộng vào phương trình thứ ba thì được:
(II) ⇔ (III)
⎧⎪⎨⎪⎩x+3y+2z=1−4y−7z=6−67z=134{x+3y+2z=1−4y−7z=6−67z=134
Hệ phương trình (III) có dạng tam giác. Tìm giá trị các ẩn ngược từ dưới lên dễ dàng tìm được nghiệm của hệ phương trình đã cho:
(x, y, z) = (-1, 2, -2)

a) Lấy (1)+(2)+(3) là tìm được z rồi thế z vào tìm x, y
b) Lấy (1) + (2) - (3) là tìm được y
\(a)\hept{\begin{cases}x-2y+z=12\\2x-y+3z=18\\-3x+3y+2z=-9\end{cases}\Leftrightarrow\hept{\begin{cases}x-2y+z=12\\3y+z=-6\\6z=21\end{cases}}}\)
\(\text{Đáp số: }(x;y;z)=(\frac{16}{3};-\frac{19}{6};\frac{7}{2})\)
\(b)\hept{\begin{cases}x+y+z=7\\3x-2y+2z=5\\4x-y+3z=10\end{cases}\Leftrightarrow}\hept{\begin{cases}x+y+z=7\\-5y-z=16\\0y+0z=-2\end{cases}}\)
\(\text{ Hệ phương trình vô nghiệm.}\)

B D C E A Q H
1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến
=> D là trung điểm của BC. Theo trên ta có góc BEC = 900.
Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.
4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).
Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)
Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3
Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.
Vậy DE là tiếp tuyến của đường tròn (O) tại E.
5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED2 = OD2 – OE2 ↔ ED2 = 52 – 32 ↔ ED = 4cm
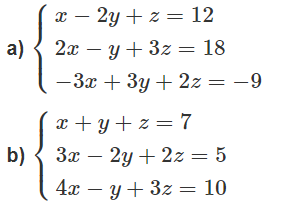 Giúp nhanh vs ạ, đng cần gấp
Giúp nhanh vs ạ, đng cần gấp
\(asinx+bcosx=c\)
\(\Leftrightarrow\frac{a}{\sqrt{a^2+b^2}}sinx+\frac{b}{\sqrt{a^2+b^2}}cosx=\frac{c}{\sqrt{a^2+b^2}}\)(1)
Có \(\left(\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\frac{b}{\sqrt{a^2+b^2}}\right)^2=1\)nên ta đặt \(\frac{a}{\sqrt{a^2+b^2}}=siny,\frac{b}{\sqrt{a^2+b^2}}=cosy\)
Phương trình (1) tương đương với:
\(sinxsiny+cosxcosy=\frac{c}{\sqrt{a^2+b^2}}\)
\(\Leftrightarrow cos\left(x-y\right)=\frac{c}{\sqrt{a^2+b^2}}\)
Nếu \(\left|\frac{c}{\sqrt{a^2+b^2}}\right|\le1\Leftrightarrow a^2+b^2\ge c^2\)phương trình có nghiệm.
Nếu \(\left|\frac{c}{\sqrt{a^2+b^2}}\right|>1\Leftrightarrow a^2+b^2< c^2\)phương trình vô nghiệm.
Em cảm ơn thầy rất nhiều ạ