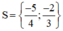Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(u=\sqrt{x+1};t=\sqrt{1-x};\text{đ}k:-1\le x\le1\)
Phương trình trở thành:
\(u+2u^2=-t^2+t+3ut\Leftrightarrow\left(u-t\right)^2+u\left(u-t\right)+\left(u-t\right)=0\)
\(\Leftrightarrow\left(u-t\right)\left(2u-t+1\right)=0\Leftrightarrow\orbr{\begin{cases}u=t\\2u+1=t\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x+1}=\sqrt{1-x}\\2\sqrt{x+1}+1=\sqrt{1-x}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{-24}{25}\end{cases}}}\)
mình dùng cách khác nhé :((
\(\sqrt{x+1}+2\left(x+1\right)=x-1+\sqrt{1-x}+3\sqrt{1-x^2}\left(đk:-1\le x\le1\right)\)
\(< =>\sqrt{x+1}-1+2x+2-3=x-1+\sqrt{1-x}-1+3\sqrt{1-x^2}-3\)
\(< =>\frac{x}{\sqrt{x+1}+1}+2x-1-x+1=-\frac{x}{\sqrt{1-x}+1}+\frac{9\left(1-x^2-1\right)}{3\sqrt{1-x^2}+3}\)
\(< =>\frac{x}{\sqrt{x+1}+1}+x+\frac{x}{\sqrt{1-x}+1}+\frac{9x^2}{3\sqrt{1-x^2}+3}=0\)
\(< =>x\left(\frac{1}{\sqrt{x+1}+1}+1+\frac{1}{\sqrt{1+x}+1}+\frac{9x}{3\sqrt{1-x^2}+3}\right)=0< =>x=0\)
rồi đến đây dùng đk đánh giá cái ngoặc khác 0 là ok


ĐK \(x\ge0\)
Đặt \(x=a,x+1=b\)
\(PT\Leftrightarrow a^4+b^4=\left(a+b\right)^4\)
<=> 4a3b+6a2b2+4ab3=0
<=> ab(2a2+3ab+2b2)=0
=>ab=0 (vì 2a2+3ab+2b2>0)
=>\(\orbr{\begin{cases}a=0\\b=0\end{cases}}\)<=>\(\orbr{\begin{cases}x=0\\x=-1\end{cases}}\)
Vậy.............................

\(\sqrt[3]{2x+1}+\sqrt[3]{x}=1\)
Đặt \(\hept{\begin{cases}\sqrt[3]{2x+1}=a\\\sqrt[3]{x}=b\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a+b=1\\a^3-2b^3=1\end{cases}}\)
\(\Rightarrow a^3-2\left(1-a\right)^3=1\)
\(\Leftrightarrow a^3-2a^2+2a-1=0\)
\(\Leftrightarrow\left(a-1\right)\left(a^2-a+1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}a=1\\b=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\sqrt[3]{2x+1}=1\\\sqrt[3]{x}=0\end{cases}}\)
\(\Leftrightarrow x=0\)
\(\sqrt[3]{2x+1}+\sqrt[3]{x}=1\)1
Đặt chug ở:\(\hept{\begin{cases}\sqrt[3]{2x+1=a}\\\sqrt[3]{x}=b\end{cases}}\)
=> Ta có:\(\hept{\begin{cases}\sqrt[a+b=1]{a^3-2b^3=1}\\\end{cases}}\)
=>\(a^3-2\left(1-a\right)^3=1\)
=>\(a^3-2a^2+2a-1=0\)
=>\(\left(a-1\right)\left(a^2-a+1=0\right)\)
=>\(\Leftrightarrow a=1;b=0\)
\(\Leftrightarrow x=0\)

Cách liên hợp
ĐK \(x\ge-2\)
PT <=> \(\sqrt{x+2}+5x+2\ne0\)
\(25x^2+19x+2+2\left(x+1\right)\left(\sqrt{x+2}-5x-2\right)=0\)
Xét \(\sqrt{x+2}+5x+2=0\)=> \(x=\frac{-19-\sqrt{161}}{50}\)
Thay vào ta thấy nó không phải là nghiệm của PT
=> \(\sqrt{x+2}+5x+2\ne0\)
<=> \(25x^2+19x+2+2\left(x+1\right).\frac{x+2-\left(5x+2\right)^2}{\sqrt{x+2}+5x+2}=0\)
<=> \(25x^2+19x+2+2\left(x+1\right).\frac{-25x^2-19x-2}{\sqrt{x+2}+5x+2}=0\)
<=> \(\orbr{\begin{cases}25x^2+19x+2=0\\1-\frac{2\left(x+1\right)}{\sqrt{x+2}+5x+2}=0\left(2\right)\end{cases}}\)
Pt (2)
<=> \(\sqrt{x+2}=-3x\)
<=> \(\hept{\begin{cases}x\le0\\9x^2-x-2=0\end{cases}}\)=> \(x=\frac{1-\sqrt{73}}{18}\)(TM ĐKXĐ)
Pt (1) có nghiệm \(x=\frac{-19+\sqrt{161}}{50}\)(Tm ĐKXĐ)
Vậy Pt có nghiệm \(S=\left\{\frac{1-\sqrt{73}}{18};\frac{-19+\sqrt{161}}{50}\right\}\)
Cách đặt ẩn phụ không hoàn toàn
ĐK\(x\ge-2\)
PT
<=> \(15x^2+6x+2\left(x+1\right)\sqrt{x+2}-\left(x+2\right)=0\)
Đặt \(\sqrt{x+2}=a\left(a\ge0\right)\)
=> \(15x^2+6x+2\left(x+1\right).a-a^2=0\)
<=> \(\left(15x^2+2ax-a^2\right)+\left(6x+2a\right)=0\)
<=> \(\left(5x-a\right)\left(3x+a\right)+2\left(3x+a\right)=0\)
<=> \(\left(3x+a\right)\left(5x-a+2\right)=0\)
<=> \(\orbr{\begin{cases}3x+a=0\\5x-a+2=0\end{cases}}\)
+ 3x+a=0
=> \(3x+\sqrt{2+x}=0\)
=> \(\hept{\begin{cases}x\le0\\9x^2-x-2=0\end{cases}}\)=> \(x=\frac{1-\sqrt{73}}{18}\)(TM ĐKXĐ)
+ 5x-a+2=0
=> \(5x+2=\sqrt{x+2}\)
=> \(\hept{\begin{cases}x\ge-\frac{2}{5}\\25x^2+19x+2=0\end{cases}}\)=> \(x=\frac{-19+\sqrt{161}}{50}\)(TM ĐKXĐ)
vậy \(S=\left\{\frac{-19+\sqrt{161}}{50};\frac{1-\sqrt{73}}{18}\right\}\)

a, Đặt \(x^2-2x=t\)
Phương trình đã cho trở thành:
\(2t^2+3t+1=0\)
Có a-b+c = 2-3+1 = 0
=> Phương trình có 2 nghiệm: \(t_1=-1;t_2=-\dfrac{1}{2}\)
Với t= -1 ta có \(x^2-2x=-1\)
\(\Leftrightarrow x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x=1\)
Với t= -1/2 ta có \(x^2-2x=-\dfrac{1}{2}\)
\(\Leftrightarrow2x^2-4x+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2+\sqrt{2}}{2}\\x=\dfrac{2-\sqrt{2}}{2}\end{matrix}\right.\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{1;\dfrac{2+\sqrt{2}}{2};\dfrac{2-\sqrt{2}}{2}\right\}\)
b, ĐK: x khác 0
Đặt \(x+\dfrac{1}{x}=t\)
Phương trình đã cho trở thành: \(t^2-4t+3=0\)
Có a+b+c=1-4+3=0
=> Phương trình có 2 nghiệm \(t_1=1;t_2=3\)
• Với t=1 ta có \(x+\dfrac{1}{x}=1\)
\(\Leftrightarrow x^2-x+1=0\)
Vì \(\Delta=1^2-4.1=-3< 0\) nên pt vô nghiệm
• Với t=3 ta có \(x+\dfrac{1}{x}=3\)
\(\Leftrightarrow x^2-3x+1=0\)
\(\Leftrightarrow x=\dfrac{3\pm\sqrt{5}}{2}\) (TMĐK)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\dfrac{3+\sqrt{5}}{2};\dfrac{3-\sqrt{5}}{2}\right\}\)
⇔ t2 – 10 = 3t ⇔ t2 – 3t – 10 = 0 (2)
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = (-3)2 - 4.1.(-10) = 49 > 0
⇒ (2) có hai nghiệm:
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm