NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ML
Em không hiểu gộp làm sao lại ra được kết quả như vậy ấy ạ.
2
13 tháng 11 2016
bạn chỉ cần bình tĩnh ,khg nên căng thẳng suy ngĩ lại những việc mình làm sai và cố gắng sửa bằng cách làm thật tốt công việc đó
chọn cho mình nhé,mình nói có đúng khg các bạn
10 tháng 9 2017
bn cần tự tin lên, đừng sa vào các thứ ko tốt cho sức khỏe, tập trung hok tập, phải độc lập lên,tao cho mik những thứ tốt đẹp nhất nhé!!! Cố lên tất cả mọi người đều tin bn
{\__ /}
* *
AH
Akai Haruma
Giáo viên
14 tháng 10 2021
Lời giải:
+ Hai cái này thực chất là 1. Chỉ khác cách tiếp cận
Hệ số góc a nói trên khía cạnh hình học. $a$ trong này có liên quan đến góc nên nó được gọi là hệ số góc của "đường thẳng" $y=ax+b$
Còn hệ số a nói trên góc độ phương trình, như em đã học ở lớp 8, nó là hệ số gắn với $x$ trong phương trình $y=ax+b$
+ Có 4 góc, nhưng ta quy ước chỉ lấy góc cắt với trục Ox ở phía trên, bên phải, tức là ở góc phần tư thứ nhất ấy.
+ Lấy ở số 1 mà không lấy ở số 0 là sao em? Khi ta vẽ điểm $(0;1)$ thì từ trục $Ox$ em lấy giá trị $x=1$, từ trục $Oy$ em lấy giá trị $y=0$ rồi dóng thẳng hai giá trị ấy để tìm điểm $A$.
AH
Akai Haruma
Giáo viên
14 tháng 7 2023
a.
$x^3-x^2-6x=0$
$\Leftrightarrow x(x^2-x-6)=0$
$\Leftrightarrow x[x(x+2)-3(x+2)]=0$
$\Leftrightarrow x(x+2)(x-3)=0$
$\Leftrightarrow x=0$ hoặc $x+2=0$ hoặc $x-3=0$
$\Leftrightarrow x=0$ hoặc $x=-2$ hoặc $x=3$
Vì $x\in\mathbb{N}^*$ nên $x=3$
Vậy $A=\left\{3\right\}$
------------------------------
b.
$(x^2-x\sqrt{3})(3x^2+5x-2)=0$
$\Leftrightarrow x(x-\sqrt{3})[x(3x-1)+2(3x-1)]=0$
$\Leftrightarrow x(x-\sqrt{3})(3x-1)(x+2)=0$
$\Leftrightarrow x=0$ hoặc $x-\sqrt{3}=0$ hoặc $3x-1=0$ hoặc $x+2=0$
$\Leftrightarrow x\in\left\{0; \sqrt{3}; \frac{1}{3}; -2\right\}$
Vì $x\in\mathbb{Q}$ nên $x\in\left\{0; \frac{1}{3}; -2\right\}$
Vậy $B=\left\{0; \frac{1}{3}; -2\right\}$
AH
Akai Haruma
Giáo viên
14 tháng 7 2023
c.
$(x-5)^2=49$
$\Leftrightarrow (x-5)^2=7^2=(-7)^2$
$\Leftrightarrow x-5=7$ hoặc $x-5=-7$
$\Leftrightarrow x=12$ hoặc $x=-2$
$x\in\mathbb{N}$ nên $x=12$
Vậy $C=\left\{12\right\}$
-------------------------------
d.
$|x|<5\Leftrightarrow -5< x< 5$
$x\in\mathbb{Z}\Rightarrow x\in\left\{-4; -3; -2; -1; 0; 1; 2;3;4\right\}$
Mà $x^2>5$ nên $x\in\left\{-4; -3; 3; 4\right\}$
Vậy $D=\left\{-4; -3; 3; 4\right\}$
4 tháng 10 2023
Câu 50 thì bạn nhóm cặp lại tan1*tan89*tan2*tan88*...*tan45
thì bạn sẽ thấy là tan1*tan89=tan2*tan88=...=tan45=1
=>D
Câu 51 thì bạn nhóm cặp lại \(sin^288^0;sin^22^0\); sin2860 và sin240;...;sin244 độ và sin2 46 độ thì bạn sẽ thấy từng cặp đó có tổng bằng 1
Và có 22 cặp như vậy nên đáp án là C
KL
1
AH
Akai Haruma
Giáo viên
30 tháng 1 2017
Lời giải:
GTLN:
Áp dụng BĐT Cauchy-Schwarz:
\(B^2=(6\sqrt{x-1}+8\sqrt{3-x})^2\leq (6^2+8^2)(x-1+3-x)=200\)
\(\Rightarrow B_{\max}= 10\sqrt{2}\Leftrightarrow \frac{3}{\sqrt{x-1}}=\frac{4}{\sqrt{3-x}}\Leftrightarrow x=\frac{43}{25}\)
GTNN:
Ta biết một bổ đề sau: Với \(a,b\geq 0\Rightarrow \sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Cách CM rất đơn giản vì nó tương đương với \(\sqrt{ab}\geq 0\) (luôn đúng)
Áp dụng vào bài toán:
\(\Rightarrow B\geq \sqrt{36x-36+192-64x}=\sqrt{156-28x}\geq 6\sqrt{2}\) (do \(x\leq 3\))
Vậy \(B_{\min}=6\sqrt{2}\Leftrightarrow x=3\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
a. Các tập thỏa mãn là tập con chứa số 2 của \(\left\{2;3;4;5;6;7\right\}\)
Số tập này bằng số tập con của \(B=\left\{3;4;5;6;7\right\}\) là tập có 5 phần tử (tìm các tập con của B, sau đó với mỗi tập con tìm được ta thêm số 2 vào là được)
\(\Rightarrow\) Có \(2^5=32\) tập thỏa mãn
(Câu a chỉ cần trình bày thế này, bỏ 2 chỗ ngoặc đơn đi là được)
b.
Tương tự, ta chỉ cần tìm tập con có 1 phần tử của \(\left\{3;4;5;6;7\right\}\)
\(\Rightarrow\) Có 5 tập thỏa mãn
Câu b có thể trình bày bằng cách liệt kê:
Các tập hợp thỏa mãn là: \(\left\{1;3\right\};\left\{1;4\right\};\left\{1;5\right\};\left\{1;6\right\};\left\{1;7\right\}\) có 5 tập thỏa mãn
(câu a có tới 32 tập nên chỉ cần biện luận, không nên liệt kê ra)
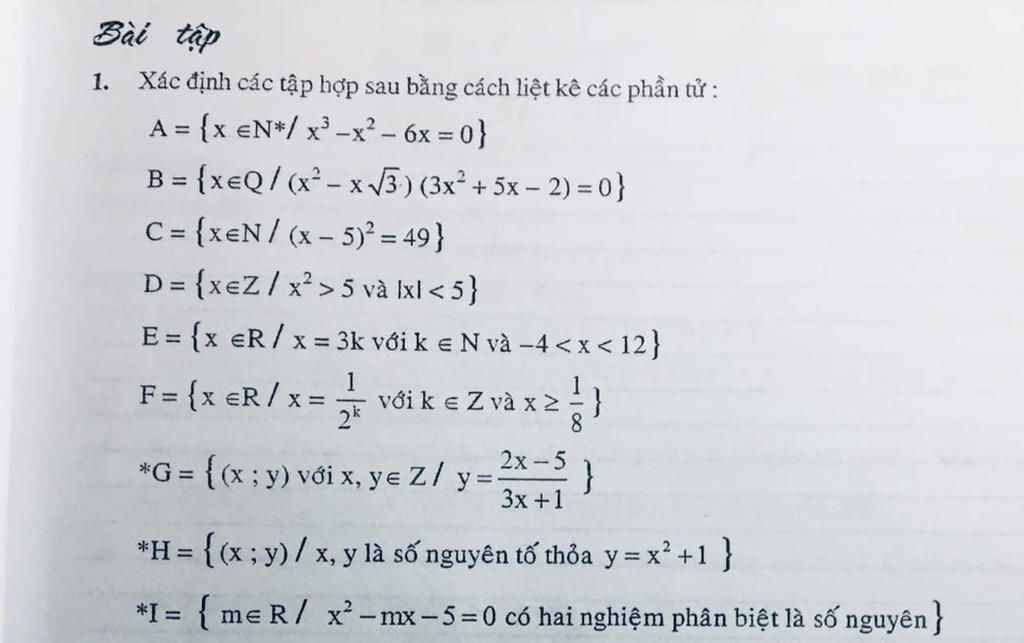
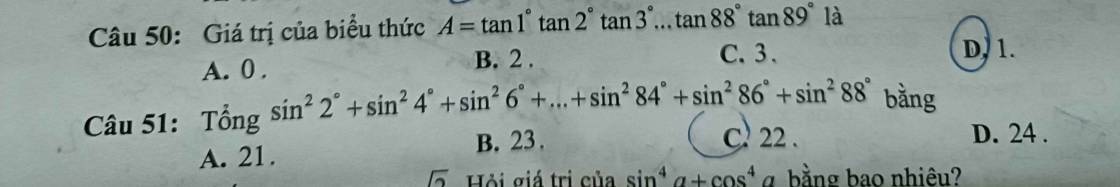
tại em non