Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điểm M nằm trong ∆ABC sao cho AM < BM thì tô phần tam giác ABC thuộc nửa mp bờ là trung trực của đoạn AB có chứa điểm A.
-Điểm M nằm trong ABC sao cho MB
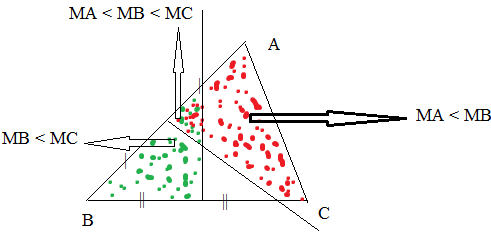
- Điểm M nằm trong ΔABC sao cho MA < MB thì tô phần ΔABC thuộc nửa mặt phẳng bờ là trung trực của đoạn AB có chứa điểm A (phần màu đỏ).
- Điểm M nằm trong ΔABC sao cho MB < MC thì tô phần ΔABC thuộc nửa mặt phẳng bờ là đường trung trực của đoạn BC có chứa B (phần màu xanh). Phần tam giác được tô hai lần (đỏ và xanh) là phần chứa điểm M thỏa: MA < MB < MC.

Áp dụng kết quả bài 70 (chương III – SGK) ta có:
MA < MB khi M thuộc nửa mặt phẳng chứa điểm A bờ là đường trung trực của AB (tô màu đỏ).
MB < MC khi M thuộc nửa mặt phẳng chứa điểm B bờ là đường trung trực của BC (tô màu xanh).
(Cách chứng minh xem lại bài 70).
Phần giao của hai nửa mặt phẳng trên là phần hình chứa điểm M thỏa mãn MA < MB < MC - chính là phần tô màu 2 lần.


a, vì M nằm ở trong tam giác ABC nên MC và MB nằm ở trong tam giác ABC
=) MC va MB lần lượt chia góc C và B làm 2 nửa
=) ^B = ^B1+ ^B2 ^C= ^C1+^C2
theo quan hệ giứa góc và cạnh đối diên có
ab tương ứng vs góc C, ac tương ứng vs góc B
MB .........................C1, MC B2
CÓ : ^B+^C > ^B2+^C2
=) AB+AC > MB+MC ( THEO QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN)
CON B THÌ CHỊU NHÉ
A B C M
a) Làm như bạn ly
b)Từ câu a) suy ra MB + MC < AB + AC;MA+MB < AC + BC
MA + MC < AB + BC
Cộng theo vế suy ra: \(2\left(MA+MB+MC\right)< 2\left(AB+BC+CA\right)\)
Suy ra \(MA+MB+MC< AB+BC+CA\) (1)
Mặt khác,áp dụng BĐT tam giácL
MB + MC > BC.Tương tự với hai BĐT còn lại và cộng theo vế: \(2\left(MA+MB+MC\right)>AB+BC+CA\)
Chia hai vế cho 2: \(MA+MB+MC>\frac{AB+BC+CA}{2}\)

B M I A C
a) Ta lần lượt xét:
- Trong \(\Delta AMI\), ta có:
\(MA< IA+IM\Leftrightarrow MA+MB< IA+IM+MB\)
\(\Leftrightarrow MA+MB< IA+IB\) (1)
- Trong \(\Delta BIC\),ta có:
\(IB< CI+CB\Leftrightarrow IA+IB< IA+CI+CB\)
\(\Leftrightarrow IA+IB< CA+CB\) (2)
Từ (1), (2), ta nhận được \(MA+MB< IA+IB< CA+CB,đpcm\)
b) Ta lần lượt xét:
- Trong \(\Delta MAB\), ta có \(MA+MB>AB\left(3\right)\)
- Trong \(\Delta MBC\), ta có \(MB+MC>BC\left(4\right)\)
- Trong \(\Delta MAC,\)ta có \(MA+MC>AC\left(5\right)\)
Cộng theo vế (3),(4),(5), ta được:
\(2\left(MA+MB+MC\right)>AB+BC+AC\)
\(\Leftrightarrow MA+MB+MC>\frac{1}{2}\left(AB+BC+AC\right),đpcm.\)
Mặt khác dựa theo kết quả cua câu a), ta có:
\(MA+MB< CA+CB\left(6\right)\)
\(MB+MC< AB+AC\left(7\right)\)
\(MA+MC< BA+BC\left(8\right)\)
Cộng theo vế (6),(7),(8), ta được:
\(2\left(MA+MB+MC\right)< 2\left(AB+BC+AC\right)\)
\(\Leftrightarrow MA+MB+MC< AB+BC+AC,đpcm.\)
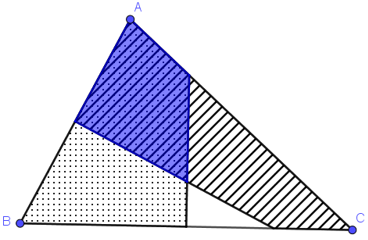
Áp dụng kết quả bài 70 (chương III – SGK) ta có:
MA < MB khi M thuộc nửa mặt phẳng chứa điểm A bờ là đường trung trực của AB (phần gạch chéo)
MB < MC khi M thuộc nửa mặt phẳng chứa điểm B bờ là đường trung trực của BC (phần được chấm chấm).
(Cách chứng minh xem lại bài 70).
Phần giao của hai nửa mặt phẳng trên là phần hình chứa điểm M thỏa mãn MA < MB < MC (phần hình được tô màu xanh).