Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi vận tốc ban đầu là x (km/h)
Đổi: 18 phút = \(\frac{3}{10}\) giờ
Thời gian đi nửa S đầu là: \(\frac{36:2}{x}=\frac{18}{x}\)
Thời gian đi nửa S sau là: \(\frac{18}{x+2}\)
Ta có phương trình: \(\frac{18}{x}+\frac{3}{10}+\frac{18}{x+2}=\frac{36}{x}\)
\(\Leftrightarrow\frac{18x+36+18x-36x-72}{x\left(x+2\right)}=\frac{-3}{10}\)
\(\Leftrightarrow-3x^2-6x+360=0\)
\(\Leftrightarrow x^2+2x-120=0\)
\(\Leftrightarrow x\left(x+2\right)=120\)
\(\Leftrightarrow\left(x-10\right)\left(x+12\right)=0\)
\(\Leftrightarrow\) \(\left[\begin{array}{nghiempt}x=10\left(TM\right)\\x=-12\left(KTM\right)\end{array}\right.\)
Vậy vận tốc ban đầu là 10 km/h
Từ tam giác đều ABC chia thành 4 tam giác đều có cạnh là 1 .
Có 5 điểm và 4 tam giác nên theo nguyên tắc Dirichlet thì có ít nhất 2 điểm nằm trong 1 tam giác đều có cạnh là 1.
Giả sử hai điểm nằm ở đầu mút hai cạnh tam giác đều cạnh 1 thì khoảng cách giữa hai điểm luôn nhỏ hơn hoặc bằng 1.
Vậy ta có điều phải chứng minh !!
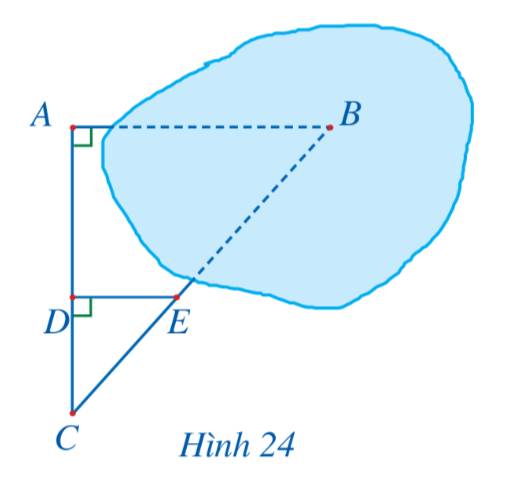
Ta có:
\(\left. \begin{array}{l}AB \bot AC\\DE \bot AC\end{array} \right\} \Rightarrow AB\parallel DE\)
Xét tam giác ABC với \(AB\parallel DE\) có:
\(\frac{{DE}}{{AB}} = \frac{{CD}}{{CA}}\) (Hệ quả của định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{18}}{{AB}} = \frac{{20}}{{50}}\\ \Rightarrow AB = 18.50:20\\ \Rightarrow AB = 45\end{array}\)
Vậy khoảng cách AB là 45m.