Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
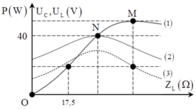
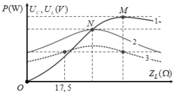
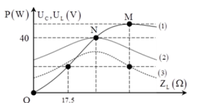
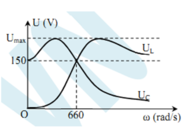
Từ đồ thị, ta thấy rằng Z L M là giá trị của cảm kháng để điện áp hiệu dụng trên cuộn dây cực đại
→ Z L M = R 2 + Z C 2 Z C
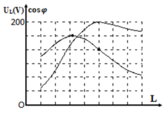
Tại N mạch xảy ra cộng hưởng, khi đó điện áp hiệu dụng trên tụ là 40 V → U C = U Z C R ↔ 40 = a Z C a → Z C = 40 Ω
Z L = 17 , 5 Ω và Z L M là hai giá trị của cảm kháng cho cùng công suất tiêu thụ.
→ Z L M + 17 , 5 = 2 Z C → Z L M = 62 , 5 Ω
Thay vào Z C và Z L M vào phương trình đầu tiên, ta tìm được a = 30
Chọn đáp án A
Từ đồ thị, ta thấy rằng 
là giá trị của cảm kháng để điện áp hiệu dụng trên cuộn dây cực đại
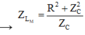
Tại N mạch xảy ra cộng hưởng, khi đó điện áp hiệu dụng trên tụ là 40 V
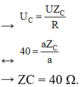
và 
là hai giá trị của cảm kháng cho cùng công suất tiêu thụ.
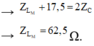
Thay vào ZC và 
vào phương trình đầu tiên, ta tìm được a = 30.
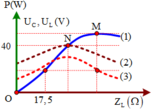
\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)
Chọn đáp án C.
L thay đổi để U C và P max khi mạch xảy ra cộng hưởng
=> Z L 0 = x 1 = Z C
+ Mặt khác khi đó ta có: Z = R
=> I = U R = 1 A
Khi đó:
U C m a x = 80 V ⇒ Z C = 80 1 = 80 Ω ⇒ x 1 = 80 Ω
+ L thay đổi với 2 giá trị Z L = 35 Ω và Z L = x 2 mạch có cùng công suất
⇒ 35 + x 2 = 2 x 1 ⇒ x 2 = 125 Ω
+ Bên cạnh đó khi Z L = x 2 là giá trị của Z L để U L m a x
125 = R 2 + Z C 2 Z C = R 2 + 80 2 80 ⇒ R = 60 Ω
