Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Gọi A là biến cố “3 đội của Việt Nam cùng nằm ở một bảng đấu”.
Ta có ![]()
Chọn ra 3 đội của Việt Nam và 1 đội khác rồi xếp chung vào 1 trong 3 bảng có: 3. C 9 1 (cách).
Chọn ra 4 đội trong 8 đội còn lại để được bảng tiếp theo có: C 8 4 (cách).
Bảng còn lại có 1 cách chọn.
![]()


Chọn A
Gọi ba bảng đấu có tên là A, B, C.
Chọn 4 đội cho bảng A có C 12 4 cách, chọn 4 đội cho bảng B có C 8 4 cách và 4 đội còn lại vào bảng C có 1 cách.
Theo quy tắc nhân, số cách chia 12 đội thành 3 bảng đấu là: (cách)
Gọi A là biến cố “3 đội Việt Nam cùng nằm ở một bảng đấu.
Giả sử 3 đội Việt Nam cùng nằm ở bảng A.
Khi đó bảng A sẽ chọn 1 đội trong 9 đội nước ngoài và 3 đội Việt Nam, 8 đội còn lại chia vào bảng B và C. Trong trường hợp này ta có số cách chọn là ![]()
Vì vai trò của các bảng là như nhau nên trường hợp 3 đội Việt Nam ở bảng B hay bảng C đều cho kết quả như nhau.
Vậy số kết quả thuận lợi cho biến cố A là ![]()
Xác suất của biến cố A là : 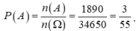

Đáp án B
Số phần tử của không gian mẫu là: ![]()
Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: ![]()
Vậy xác suất cần tính
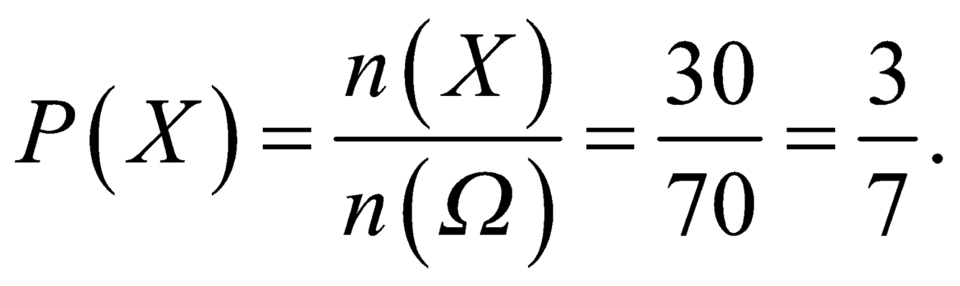

1. Không gian mẫu: \(C_{12}^4C_8^4C_4^4\)
Xếp 3 đội Việt Nam vào 3 bảng: \(3!=6\) cách
Còn 9 đội nước ngoài, có \(C_9^3C_6^3C_3^3\) cách xếp
Xác suất: \(P=\dfrac{6.C_9^3C_6^3C_3^3}{C_{12}^4C_8^4C_4^4}=...\)
2.
Không gian mẫu: \(C_{11}^2\)
Tích 2 số chẵn khi có ít nhất 1 số chẵn
Số cách chọn 2 thẻ đều lẻ: \(C_6^2\)
Số cách chọn ít nhất 1 thẻ chẵn: \(C_{11}^2-C_6^2\)
Xác suất: \(P=\dfrac{C_{11}^2-C_6^2}{C_{11}^2}=...\)
https://hoc24.vn/cau-hoi/bai-1-cho-tam-giac-abc-co-ba-goc-nhon-ke-hai-duong-cao-bd-va-ce-goi-m-n-lan-luot-la-hinh-chieu-cua-bc-tren-duong-thang-de1tu-giac-bmnc-la-hinh-givi-sao2goi-o-la-trung-diem-cua-doan-tha.329689210002 cho e spam xíu ạ , giúp e với

Chuyên đề [url=http://toancap3.com/chuyen-de/to-hop-va-nhi-thuc-newton/]tổ hợp và nhị thức newton[/url]

Đáp án C
Cách chia 9 đội ra thành 3 bảng là
![]()
Cách chia 3 đội bóng của Việt Nam ở 3 bảng khác nhau là
![]()
⇒ p = 540 1680 = 9 28

Đáp án B
Số cách sắp ngẫu nhiên là C 9 3 . C 6 3 . C 3 3 = 1680 (cách).
Số cách sắp để ba đội của Việt Nam ở 3 bảng khác nhau là
( C 6 2 C 3 1 ) ( C 4 2 C 2 1 ) ( C 2 2 C 2 1 ) = 540 cách.
Xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: 540 1680 = 9 28 .