Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu đầu tiên của đề bài là "Với mọi \(n\inℤ^+\)..." chứ không phải \(m\) nhé, mình gõ nhầm.
a) Ta phân tích \(n=x_1^{a_1}.x_2^{a_2}...x_m^{a_m}\) (với \(x_1;x_2;..x_n\) là số nguyên tố ;
\(a_1;a_2;..a_m\inℕ^∗\) và là số mũ tối đa của mỗi số nguyên tố )
Khi đó ta có \(\sigma\left(n\right)=\left(a_1+1\right)\left(a_2+1\right)...\left(a_m+1\right)\)
mà \(\sigma\left(n\right)\) lẻ \(\Leftrightarrow\) \(a_1+1;a_2+1;...a_m+1\) lẻ
\(\Leftrightarrow a_1;a_2;..a_m\) chẵn
\(\Leftrightarrow n\) là số chính phương
=> n luôn có dạng \(n=l^2\)
Mặt khác \(x_1;x_2;..x_m\) là số nguyên tố
Nếu \(x_1;x_2;..x_m\) đều là số nguyên tố lẻ thì l lẻ
<=> r = 0 nên n = 2r.l2 đúng (1)
Nếu \(x_1;x_2;..x_m\) tồn tại 1 cơ số \(x_k=2\)
TH1 : \(a_k\) \(⋮2\)
\(\Leftrightarrow a_k+1\) lẻ => \(\sigma\left(n\right)\) lẻ (thỏa mãn giả thiết)
=> n có dạng n = 2r.l2 (r chẵn , l lẻ)(2)
TH2 : ak lẻ
Ta dễ loại TH2 vì khi đó \(a_k+1⋮2\) nên \(\sigma\left(n\right)⋮2\) (trái với giả thiết)
Nếu \(n=2^m\) (m \(⋮2\)) thì r = m ; l = 1 (tm) (3)
Từ (1);(2);(3) => ĐPCM

Điều kiện: 3 x 2 + 7 x ≥ 0 3 x − 1 ≥ 0 ⇔ x ≥ 1 3 *
Với điều kiện trên, phương trình tương đương
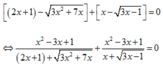
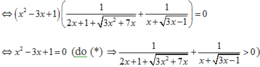
![]()
Theo yêu cầu đề bài ta chọn nghiệm x = 3 + 5 2
Vậy a = 3 , b = 5 , c = 2 ⇒ S = a + b + c = 10
Đáp án cần chọn là: C

a) \(det=\left|\begin{matrix}1&-m\\m&1\end{matrix}\right|=1+m^2\ne0\) với mọi m => Hệ phương trình bậc nhất hai ẩn luôn có nghiệm
b) Ta có:
x0 - my0 = 2 - 4m
mx0 + y0 = 3m + 1
Hay là:
x0 - 2 = m (y0 - 4)
y0 - 1 = m (3 - x0)
=> Chia hai vế cho nhau ta được
\(\frac{x_0-2}{y_0-1}=\frac{y_0-4}{3-x_0}\)
=> (x0 - 2)(3 - x0) = (y0 - 4)(y0 - 1)
=> -x02 + 5x0 - 6 = y02 - 5y0 + 4
=> x02 + y02 - 5(x0 + y0) = -10
ĐPCM