Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(Ghi chú: Muốn chứng minh hai số là nghịch đảo của nhau, ta chứng minh tích của hai số bằng 1.)

Ủa đề là j vậy bạn . @Nguyen Duc Hieu
Nếu là đề yêu cầu chứng minh ( vì trong sgk toán 9 có ) thì làm như sau :
Đề :
Chứng minh
a) (2 - √3)(2 + √3) = 1;
b) (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau.
----------------------------------------------------------------------------------------------------------------------------------
a) \(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=1\)
Ta biến đổi vế trái :
\(VT=\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=4+2\sqrt{3}-2\sqrt{3}-\sqrt{3^2}=4-3=1\)
b) \(\left(\sqrt{2006}-\sqrt{2005}\right)v\text{à}\left(\sqrt{2006}+\sqrt{2005}\right)\)
Ta có : Nếu : ( \(\sqrt{2006}-\sqrt{2005}\) )( \(\sqrt{2006}+\sqrt{2005}\) ) =1 thì (√2006 - √2005) và (√2006 + √2005) là hai số nghịch đảo của nhau.
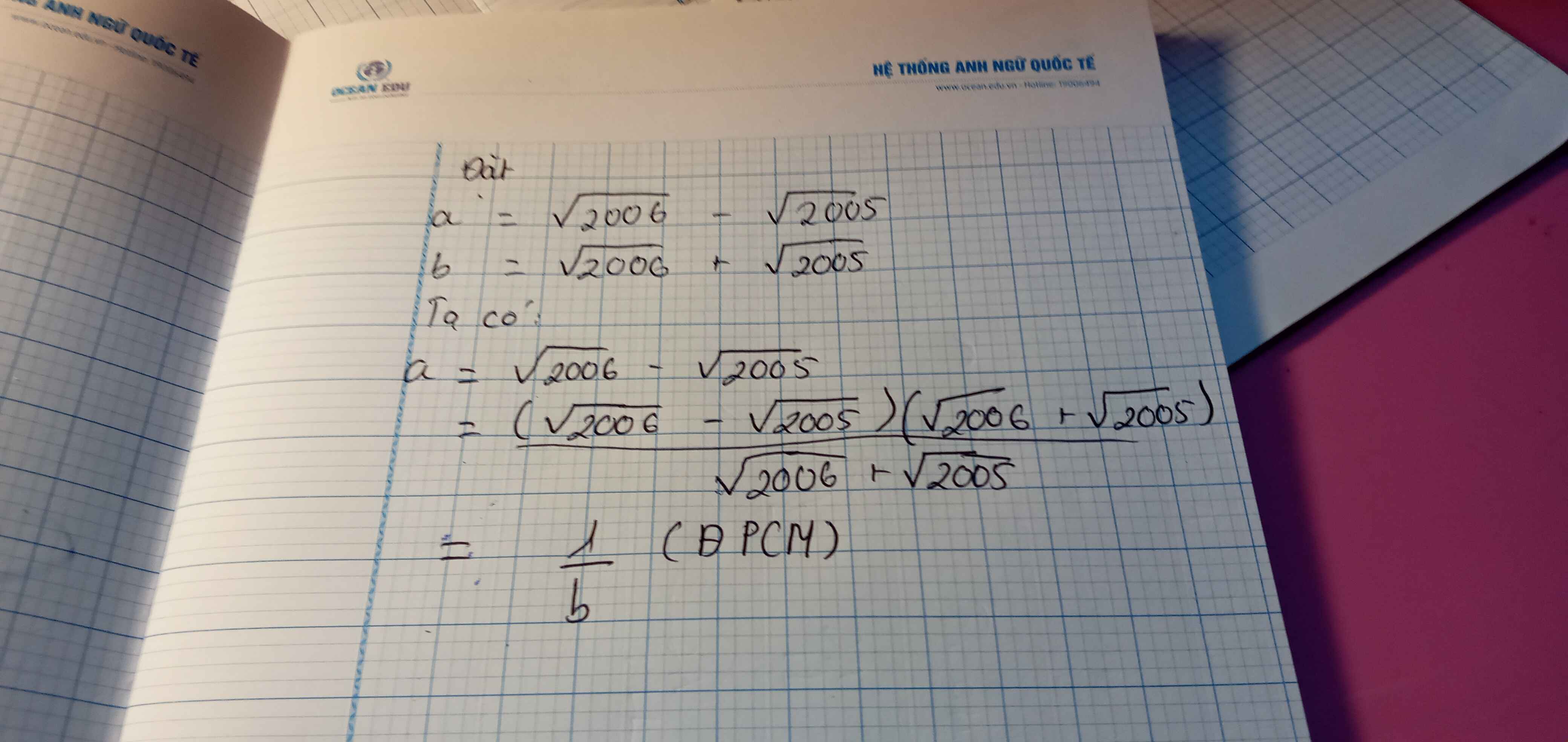
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)

\(\left(x-\sqrt{11}\right)^2=0\)
\(\left(x-\sqrt{11}\right)=0\)
\(x=\sqrt{11}\)
\(\left(x-\sqrt{11}^2=0\right)\)
\(\left(x-\sqrt{11}\right)=0\)
\(x=\sqrt{11}\)

Đặt \(a=\sqrt{2006}-\sqrt{2005}\) , \(b=\sqrt{2006}+\sqrt{2005}\)
Ta sẽ chứng minh \(a=\frac{1}{b}\)
Ta có : \(a=\sqrt{2006}-\sqrt{2005}=\frac{\left(\sqrt{2006}-\sqrt{2005}\right).\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\frac{2006-2005}{\sqrt{2006}+\sqrt{2005}}\)
\(=\frac{1}{\sqrt{2006}+\sqrt{2005}}=\frac{1}{b}\)
Vậy a và b là hai số nghịch đảo.
Đầu tiên nhắc lại định nghĩ hai số nghịch đảo: Hai số được gọi là nghịch đảo nếu tích của chúng bằng 1.
Vd: $ab=1\implies $ a và b là hai số nghịch đảo của nhau và ngược lại nếu a và b là hai số nghịch đảo của nhau thì $ab=1$.
Áp dụng vào bài toán trên ta có: $(\sqrt{2006}-\sqrt{2005})(\sqrt{2006}-\sqrt{2005})=1\implies $ hai số trên là nghịch đảo của nhau.

Sửa đề:
\(VP=\sqrt{1+2005^2+\dfrac{2005^2}{2006^2}}+\dfrac{2005}{2006}\)
Ta có: \(2005^2+1=\left(2005+1\right)^2-2.2005.1=2006^2-2.2005\)
\(\Rightarrow VP=\sqrt{2006^2-2.2005+\dfrac{2005^2}{2006^2}}+\dfrac{2005}{2006}\)
\(=\sqrt{\left(2006-\dfrac{2005}{2006}\right)^2}+\dfrac{2005}{2006}\)
\(=2006-\dfrac{2005}{2006}+\dfrac{2005}{2006}=2006\)
Phương trình đã cho tương đương
\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=2006\)
\(\Leftrightarrow\sqrt{\left(x-1\right)^2}+\sqrt{\left(x-2\right)^2}=2006\)
\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=2006\)
Đến đây thì tự xét trường hợp và giải tìm nghiệm, bài này không cần điều kiện nhé

x-2006=y
I(y+1)I^2005+IyI^2006=1
=> y=0, y=-1
x=2006 hoac x=2005
Hằng đẳng thức a2 - b2 = (a - b).(a + b) <=> (a - b).(a + b) = a2 - b2
bạn nên hỏi luôn khi cô giảng chứ, đừng giấu dốt nhé