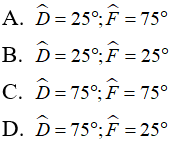Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

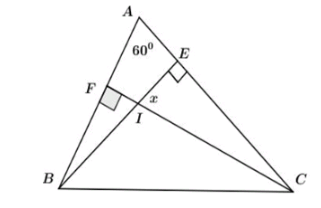
Câu 1 lỗi font còn câu 2 là 60 độ nhé do x và góc A đều bù góc FIE
Bài 9: Cho tam giác DEF có D^ - F^ = 50° và E^ = 80°. Số đo của góc D^ và F^ lần lượt là?

a) Ta có D^+E^+F^=1800 nên F^=1800−D^−E^=1800−1020−250=530.
b) Ta có D^+E^+F^=1800⇒2x+360+x=1800⇒3x=1440⇒x=480.
Vậy F^=480;D^=2.480=960.
c) Ta có D^+E^+F^=1800⇒E^+F^=1800−D^=1800−32=1480.
Lại có F^−E^=240 nên F^=(1480+240):2=860;E^=1480−860=620

a) Góc C có độ là :
\(180^o-\left(30^o+65^o\right)=85^o\)
b) Góc F có độ là ;
\(180^o-\left(35^o+60^o\right)=85^o\)

\(\text{Câu 1: }=\widehat{B}+\widehat{C}=80^0\left(D\right)\\ \text{Câu 2:}\Delta ABC=\Delta DEF\left(A\right)\)

A B C D E F I
a,
ta có
A + B+ C = \(180^0\)
B + C = \(180^0\)- A
mà BI là phân giác góc B
IBC = \(\frac{1}{2}\)B
CI là phân giác góc C
ICB = \(\frac{1}{2}\)C
suy ra
IBC + ICB = \(\frac{1}{2}\)B + \(\frac{1}{2}\)C = \(\frac{1}{2}\)( B + C ) = \(\frac{1}{2}\)( \(180^0\)- A ) = \(\frac{1}{2}\) \(\left(180^0-60^0\right)\)= \(60^0\)
mà IBC + ICB + BIC = \(180^0\)
suy ra BIC = \(180^0\)- ( IBC + ICB )
BIC = \(180^0\)- \(60^0\)
BIC = \(120^0\)
b,
ta có vì I là giao điểm của phân giác góc B và C
suy ra phân giác góc A đi qua I suy ra tia AI trùng tia IF suy ra AF là phần giác góc A mà I cách đều AB ; AC ; BC
nên IE = ID = IF
c,
ta có EIB + BIC =\(180^0\)
EIB = \(180^0-120^0\)
EIB = \(60^0\)
Mà EIB đối đỉnh góc DIC
suy ra DIC = EIB = \(60^0\)
vì IF là tia phân giác góc BIC
nên BIF = CIF = \(\frac{1}{2}\)\(120^0\)= \(60^0\)
EIF = BIE + BIF = \(60^0+60^0=120^0\)
DIF = DIC + CIF = \(60^0+60^0=120^0\)
xét tam giác EIF và DIF có
EIF = DIF = \(120^0\)
IF là cạnh chung
IE = ID
suy ra tam giác EIF = tam giác DIF ( c-g-c )
suy ra EF = DF
ta có góc BIC đối đỉnh góc EID
nên BIC = EID = \(120^0\)
xét tam giác EIF và EID có
EID = EIF =\(120^0\)
ID = IF
IE cạnh chung
suy ra tam giác DIE = tam giác FIE ( c-g-c )
suy ra ED = EF
mà EF = DF
suy ra ED = EF = DF
suy ra tam giác EDF là tam giác đều
d,
ta có IE = IF = ID
nên I cách đều 3 đỉnh tam giác DFE nên I là giao điểm của 3 đường trung trực tam giác DEF
mà trong tam giác đều 3 đường trung trực đồng thời là 3 đường phân giác của tam giác đó
suy ra I là giao điểm của hai đường phân giác trong tam giác ABC vá DEF