Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C O H D E F
Ta có: Tứ giác ABDC nội tiếp đường tròn (O) => ^DBC=^CAD (1)
Đường tròn (O) có đường kính AD và điểm B thuộc (O) => ^ABD vuông tại B => AB \(\perp\)BD
=> HE // BD (Quan hệ song song vuông góc) => ^DBC=^BHE (So le trong)
^BHE=^BAH (Cùng phụ ^AHE) => ^DBC=^BAH=^EAH.
Dễ thấy tứ giác AEHF là tứ giác nội tiếp (Tâm là trung điểm của AH)
=> ^EAH=^EFH. Mà ^EAH=^DBC (cmt) => ^EFH=^DBC (2)
Từ (1) và (2) => ^CAD=^EFH
Lại có: ^EFH+^AFE=900 ; ^CAD+^ADC=900 => ^AFE=^ADC
=> ^CAD+^AFE=900 => AD\(\perp\)EF (đpcm)

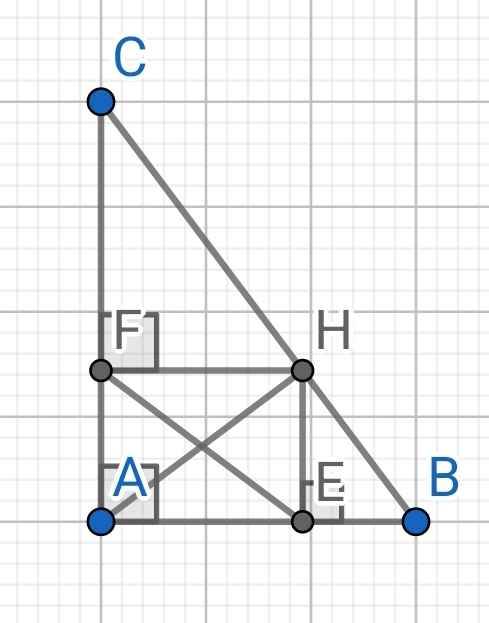
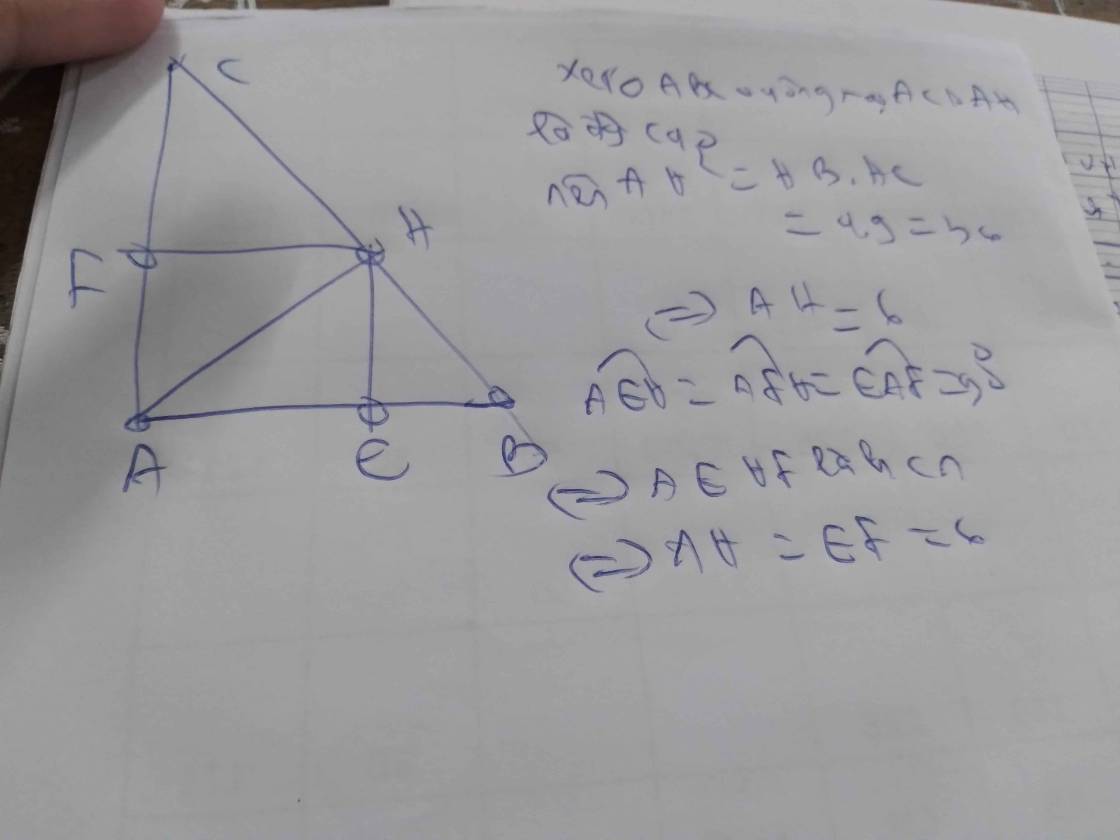
ABC vuông tại A có AH là đường cao
⇒AH² = HB . HC
= 4 . 9
= 36
⇒ AH = 6
Tứ giác AEHF có:
∠HEA = ∠FAE = ∠AFH = 90⁰
⇒ AEHF là hình chữ nhật
⇒ EF = AH = 6

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=1.8\cdot3.2=5.76\)
hay AH=2,4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=1.8\cdot5=9\\AC^2=3.2\cdot5=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=3\left(cm\right)\\AC=4\left(cm\right)\end{matrix}\right.\)

a: BC=BH+CH
=2+8
=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{2\cdot8}=4\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{2\cdot10}=2\sqrt{5}\left(cm\right)\\AC=\sqrt{8\cdot10}=4\sqrt{5}\left(cm\right)\end{matrix}\right.\)
b: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>DE=AH
c: ΔHDB vuông tại D
mà DM là đường trung tuyến
nên DM=HM=MB
\(\widehat{EDM}=\widehat{EDH}+\widehat{MDH}\)
\(=\widehat{EAH}+\widehat{MHD}\)
\(=90^0-\widehat{C}+\widehat{C}=90^0\)
=>DE vuông góc DM

a) tam giác ABC vuông tại A nên áp dụng Py-ta-go:
\(\Rightarrow AC^2=BC^2-AB^2=25^2-15^2=400\Rightarrow AC=20\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{15.20}{25}=12\left(cm\right)\)
b) tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{15^2}{25}=9\left(cm\right)\)
tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AH.HB=HE.AB\Rightarrow HE=\dfrac{AH.HB}{AB}=\dfrac{12.9}{15}=\dfrac{36}{5}\left(cm\right)\)
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHC vuông tại H có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AC=AH^2=AE.AB\)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=25^2-15^2=400\)
hay AC=20(cm)
c) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

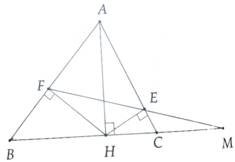
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)
Mình nghĩ phải là \(HB.HC=4OE^2\) mới đúng.
Dễ thấy tứ giác AEHF là hình chữ nhật do có \(\widehat{EAF}=\widehat{AEH}=\widehat{AFH}=90^o\)
Do đó \(EF=AH\) (2 đường chéo của hình chữ nhật thì bằng nhau) và \(AH=EF=2OE\) (do 2 đường chéo của hình chữ nhật cắt nhau tại trung điểm mỗi đoạn)
Tam giác ABC vuông tại A có đường cao AH nên \(HB.HC=AH^2\) \(\Rightarrow HB.HC=\left(2OE\right)^2=4OE^2\) (đpcm)
HE vuông góc vs AB nha giúp mik vs