Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M D E I
a, Vì AD // BM (gt) => góc DAB = góc ABM (so le trong)
Xét t/g IAD và t/g IBM có:
IA = IB (gt)
góc DAB = góc ABM
AD = BM (gt)
=> t/g IAD = t/g IBM (c.g.c)
=> góc DIA = góc BIM (2 góc t/ứ), ID = IM
Mà góc DIA + góc DIB = 180 độ (kề bù)
=> góc DIB + góc BIM = 180 độ
=> góc DIM = 180 độ
=> D,I,M thẳng hàng
b, Xét t/g AIM và t/g BID có:
IA = IB (gt)
góc DIB = góc MIA (đối dỉnh)
ID = IM (câu a)
=> t/g AIM = t/g BID (c.g.c)
=> góc IMA = góc BDI (2 góc t/ứ)
=> AM // DB (1)
c, Vì AE // MC => góc EAC = góc ACM (so le trong)
Xét t/g AEC và t/g CMA có:
AE = MC (gt)
góc EAC = góc ACM
AC chung
=> t/g AEC = t/g CMA (c.g.c)
=> góc MAC = góc ACE (2 góc t/ứ)
=> AM // CE (2)
Từ (1) và (2) => DB // CE

Câu a)
Cách khác
Xét tứ giác ADBM có :
AD // BM ( GT )
AD = BM ( GT )
=> tứ giác ADBM là hình bình hành
Mà I là trung điểm AB ( GT )
=> I là trung điểm DM
=> 3 điểm D,I,M thẳng hàng

a )
Xét \(\Delta AID\)và \(\Delta BIM\) có :
AI=IB (do I là trung điểm AB)
\(\widehat{DAI}=\widehat{IBM}\) (do AD//BM mà 2 góc ở vị trí so le trong)
AD=BM (GT)
Suy ra : ΔAID=ΔBIM (c.g.c) (1)
\(\Rightarrow\widehat{AID}=\widehat{BIM}\) (2 góc tương ứng)
Do vậy, M, I, D thẳng hàng
b,
Từ (1) \(\Rightarrow\widehat{ADI}=\widehat{IMB}\)(2 góc tương ứng)
Mà 2 góc trên ở vị trí so le trong nên AM//DB
c,
Xét\(\Delta AEC\)và \(\Delta CMA\) có:
AC: cạnh chung
\(\widehat{EAC}=\widehat{ACM}\)(do AE//BC)
AE=MC (cùng bằng BM)
Suy ra ΔAEC=ΔCMA (c.g.c)
\(\Rightarrow\widehat{MAC}=\widehat{ECA}\)2 góc tương ứng)
Mà 2 góc trên ở vị trí so le trong nên EC//DB

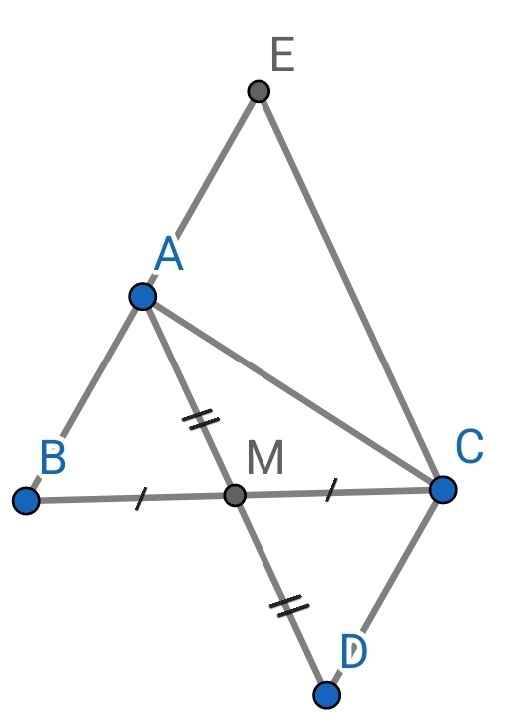 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE

a: Xét tứ giác AMBD có
AD//BM
AD=BM
Do đó: AMBD là hình bình hành
Suy ra: HAi đường chéo BA và MD cắt nhau tại trung điểm của mỗi đườg
=>I là trung điểm của MD
hay D,I,M thẳng hàng
b: Vì AMBD là hình bình hành nên AM//BD
c: Ta có: AD=BM
AD=AE
nên AE=BM
mà BM=BC/2
nên AE=BC/2
=>ED=BC
Xét tứ giác BDEC có
DE//BC
DE=BC
Do đó: BDEC là hình bình hành
Suy ra: EC//BD

Câu a thui
A, Xét Tam giác ABC và Tam giác AED có
AB=AD
BD cạnh chung
AC=AE
=>TAM GIÁC ABC=TAM GIÁC AED