Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
A B C O I K H Q D
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

Cho tam giác ABCABC không có góc tù (AB < AC)(AB<AC), nội tiếp đường tròn (O; R)(O;R), (BB, CC cố định, AA di động trên cung lớn BC). Các tiếp tuyến tại BB và CC cắt nhau tại MM. Từ MM kẻ đường thẳng song song với ABAB, đường thẳng này cắt (O)(O) tại DD và EE (DD thuộc cung nhỏ BCBC), cắt BCBC tại FF, cắt ACAC tại II. Chứng minh rằng \widehat{MBC}=\widehat{BAC}MBC=BAC . Từ đó suy ra MBICMBIC là tứ giác nội tiếp.
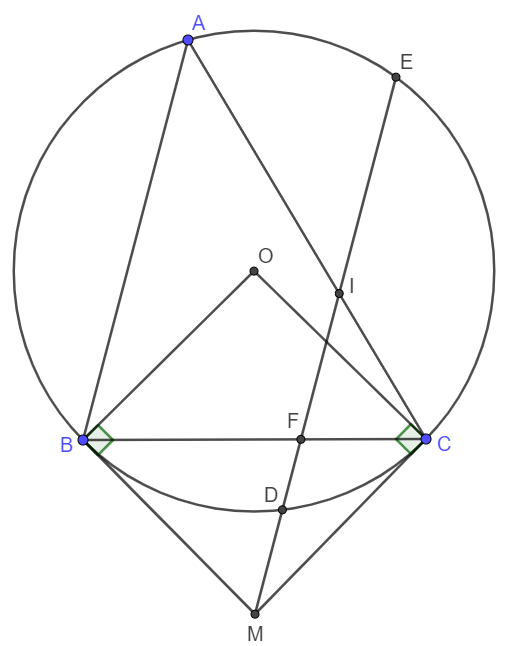
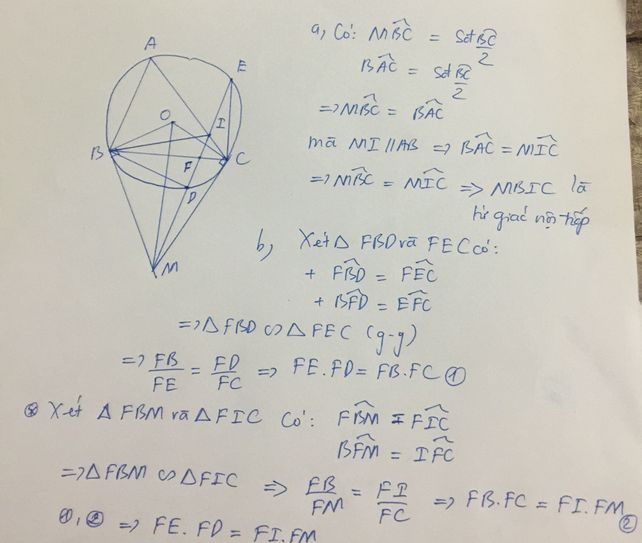
theo gt, ta co:
goc MBC= BAC (cung chan cung BC)
mat khac, ta lai co goc BAC = MIC ( dong vi)
=> goc MBC= MIC
=> tu giac BICM noi tiep

b, Vì DF//AB nên \(\widehat{DHC}=\widehat{BAC}\)(đồng vị)
mà \(\widehat{BAC}=\frac{1}{2}\widehat{BOC}=\widehat{DOC}\)(góc nội tiếp và góc ở tâm)
\(\Rightarrow\widehat{DOC}=\widehat{DHC}\)hay tứ giác DOHC nội tiếp
\(\Rightarrow\widehat{DHO}=\widehat{DCO}=90^0\)\(\Rightarrow OH\perp DF\)
câu c tí nữa làm :P
c, Từ a, b => 5 điểm B,O,H,C,D cùng nằm trên đường tròn đường kính OD
Vì tứ giác BHCD nội tiếp \(\Rightarrow ID.IH=IB.IC\)
Vì tứ giác BECF nội tiếp \(\Rightarrow IE.IF=IB.IC\)
\(\Rightarrow ID.IH=IE.IF\)

A B C M O D E F I P Q T
1) Ta có 4 điểm B,O,C,M cùng thuộc đường tròn đường kính OM (^MBO = ^MCO = 900) (1)
Do MI // AB và MB tiếp xúc với (O) tại B nên ^CIM = ^CAB = ^CBM
=> 4 điểm B,I,C,M cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra 5 điểm M,B,O,I,C cùng thuộc một đường tròn (đpcm).
2) Theo câu a thì M,B,I,C cùng thuộc (OM), có BC giao IM tại F => FI.FM = FB.FC
Đường tròn (O) có dây BC giao DE tại F nên FB.FC = FD.FE
Do vậy FI.FM = FD.FE => \(\frac{FI}{FE}=\frac{FD}{FM}\) (đpcm).
3) Điểm I thuộc đường tròn (OM) => ^OIM = 900 hay ^QIM = 900
Dễ thấy FQ.FT = FB.FC = FI.FM, suy ra tứ giác QMTI nội tiếp => ^QTM = ^QIM = 900
=> \(\Delta\)QTM vuông tại T. Theo ĐL Pytagoras: \(TQ^2+TM^2=QM^2\)
Vậy thì \(\frac{TQ^2+TM^2}{MQ^2}=1.\)

A B C O D E K M F T y x
c) Gọi T là giao điểm thứ hai của FD với đường tròn (O). Ta c/m EO đi qua T.
Ta có: ^ADM = ^DAC + ^DCA = ^BAC/2 + ^ACB = ^BAD + ^MAB = ^MAD => \(\Delta\)DAM cân tại M => MA=MD
Lại có: MA và MF là 2 tiếp tuyến của (O) nên MA=MF. Do đó: MD=MF => \(\Delta\)MDF cân tại M (đpcm).
Dễ thấy: \(\Delta\)MAB ~ \(\Delta\)MCA (g.g) và \(\Delta\)MFB ~ \(\Delta\)MCF (g.g)
=> \(\frac{MA}{MC}=\frac{MF}{MC}=\frac{AB}{AC}=\frac{BD}{CD}=\frac{FB}{FC}\) => FD là tia phân giác ^BFC (1)
Kẻ tia đối Fy của FB => ^EFy = ^ECB = ^EBC = ^EFC => FE là phân giác ^CFy (2)
Từ (1) và (2) suy ra: FD vuông góc với FE (Vì ^BFC + ^CFy = 1800) hay ^EFT = 900
=> ET là đường kính của (O) => ET trùng với OE => OE đi qua T => ĐPCM.
d) Áp dụng ĐL Ptolemy có tứ giác BFCT nội tiếp có: BF.CT + CF.BT = BC.FT
=> CT.(BF+CF) = BC.FT => \(BF+CF=\frac{BC.FT}{CT}\le\frac{BC.ET}{CT}=\frac{2CK.ET}{CT}=2EC=2BE\)
Dấu "=" xảy ra khi F trùng với E <=> MF vuông góc OE <=> MF // BC => M không nằm trên BC (mâu thuẫn)
=> Không có dấu "=" => BF+CF < 2BE (đpcm).
 đây nha bn
đây nha bn