Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Hai tam giác vuông \(AEC,AFB\) có chung góc nhọn đỉnh A nên đồng dạng với nhau. Suy ra \(\frac{AE}{AF}=\frac{AC}{AB}\to\Delta AEF\sim\Delta ABC\left(c.g.c\right)\). Từ đây, sử dụng tính chất tỉ số diện tích bằng bình phương tỉ số đồng dạng, cho ta \(\frac{S_{AEF}}{S_{ABC}}=\left(\frac{AE}{AB}\right)^2=\left(\cos\angle BAC\right)^2.\)
b. Xét hai tam giác \(\Delta KMN,\Delta BHA\) có \(KM\parallel BA,KN\parallel BH,MN\parallel AH\to\Delta KMN\sim\Delta BHA\left(g.g\right)\) (các góc tạo bởi các cạnh tương ứng song song thì bằng nhau). Đặc biệt ta suy ra \(\frac{KM}{KN}=\frac{BH}{BA}\to BH\cdot KM=BA\cdot KN.\)
c. Theo câu b., vì hai tam giác \(\Delta KMN,\Delta BHA\) đồng dạng nên \(\frac{KN}{BH}=\frac{MN}{AH}=\frac{1}{2}\to\) theo định lý Ta-let, đường thẳng KB cắt HN ở điểm G' sao cho \(\frac{G'N}{G'H}=\frac{1}{2}.\) Suy ra G' là trọng tâm tam giác AHC. Mặt khác theo giả thiết G là giao điểm của HN và AM, là hai trung tuyến của tam giác AHC. Suy ra G cũng là trọng tâm tam giác AHC. Vậy G và G' trùng nhau. Đặc biệt ta suy ra \(K,G,B\) thẳng hàng.
Theo tính chất trọng tâm và định lý Ta-let, ta có \(\frac{GA}{GM}=\frac{GB}{GK}=\frac{GH}{GN}=2\to\left(\frac{GA}{GM}\right)^5=\left(\frac{GB}{GK}\right)^5=\left(\frac{GH}{GN}\right)^5=32\)
Do đó theo tính chất tỉ lệ thức: \(\left(\frac{GA}{GM}\right)^5=\left(\frac{GB}{GK}\right)^5=\left(\frac{GA}{GN}\right)^5=32=\frac{GA^5+GB^5+GH^5}{GM^5+GK^5+GN^5}\)
Suy ra \(\sqrt{\frac{GA^5+GB^5+GH^5}{GM^5+GK^5+GN^5}}=\sqrt{32}=4\sqrt{2}.\) (ĐPCM)

Câu hỏi của Diệp Song Thiên - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo link này nhé!

Giải chi tiết:
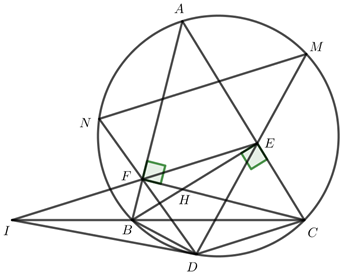
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.

Em đã học tứ giác nội tiếp chưa? Nếu học rồi áp dụng nó sẽ nhanh hơn.
A B C H D E F I N M O
Gọi H là trực tâm tam giác ABC.
+) Ta có: AM//NH ( cùng vuông góc với AB)
AN// MH ( cùng vuông góc với AC)
=> AMHN là hình bình hành
Gọi O là giao điểm của AH và MN
=> O là trung điểm AH
+) Xét tứ giác BFHD có: \(\widehat{FBD}+\widehat{FHD}+\widehat{BFH}+\widehat{BDH}=360^o\)
=> \(\widehat{FBD}+\widehat{FHD}+90^o+90^o=360^o\)
=> \(\widehat{FBD}+\widehat{FHD}=180^o\)
Mà \(\widehat{FHD}+\widehat{FHA}=180^o\)( kề bù)
=> \(\widehat{FBD}=\widehat{FHA}\)
Mặt khác\(\widehat{FHA}=\widehat{HAM}\) ( so le trong)
=> \(\widehat{FBD}=\widehat{HAM}\)
=> \(\widehat{ABC}=\widehat{HAM}\)(1)
Xét tứ giác HDCE có:
\(\widehat{DCE}+\widehat{DHE}+\widehat{HDC}+\widehat{HEC}=360^o\)
=> \(\widehat{DCE}+\widehat{DHE}+90^o+90^o=360^o\)
=> \(\widehat{DCE}+\widehat{DHE}=180^o\)
Mà \(\widehat{AHM}+\widehat{EHD}=180^o\)( kề bù)
=> \(\widehat{AHM}=\widehat{DCE}\Rightarrow\widehat{AHM}=\widehat{ACB}\)(2)
Từ (1), (2) => Tam giác MAH ~ Tam giác ABC
=> \(\frac{MA}{AH}=\frac{AB}{BC}\Rightarrow\frac{MA}{2.AO}=\frac{AB}{2BI}\Rightarrow\frac{MA}{AO}=\frac{AB}{AI}\)(3)
Từ (1), (3)=> Tam giác MAO ~ tam giác ABI
=> \(\widehat{OMA}=\widehat{IAB}\)
Ta lại có: \(\widehat{IAB}+\widehat{IAM}=\widehat{BAM}=90^o\)
=> \(\widehat{OMA}+\widehat{IAM}=90^o\)
Gọi K là giao điểm của MN và AI
=> \(\widehat{KMA}+\widehat{KAM}=90^o\)
=> \(\widehat{AKM}=90^o\)
=> AI vuông MN
cái chỗ \(\frac{MA}{2AO}\)= \(\frac{AB}{2BI}\)\(\Rightarrow\frac{MA}{AO}=\frac{AB}{AI}\)
Nhg \(\frac{MA}{2AO}\) = \(\frac{AB}{2BI}\)\(\Rightarrow\frac{MA}{AO}=\frac{AB}{BI}\)
#MÃ MÃ#
ngu
saint suppapong udomkaewkanjanaUnruly KidĐP Nhược GiangNgô Kim TuyềnNgô Thành ChungNguyễn Thanh HằngMashiro ShiinaFa Châu DeMysterious PersonJakiNatsumiDƯƠNG PHAN KHÁNH DƯƠNGArakawa WhiterAkai Haruma
Hộ em với :<<<