Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.
Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C
dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)
Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.
Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).
Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).
Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.
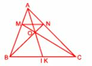
b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).
Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)
Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).
Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.

A B C M G N
a) Xét tam giác ABG và tam giác BGM có chung đường cao hạ từ B xuống đáy AM
Mà \(AG=2GM\) \(\Rightarrow S_{\Delta AGB}=2S_{\Delta BGM}\)
\(\Rightarrow S_{\Delta BGM}=\frac{1}{2}S_{\Delta AGB}=\frac{1}{2}\times20=10\left(cm^2\right)\)
Ta có \(S_{\Delta ABM}=S_{\Delta ABG}+S_{\Delta BGM}=20+10=30\left(cm^2\right)\)
Xét \(\Delta ABM\)và \(\Delta ACM\)có chung đường cao hạ từ A xuống cạnh đáy
Mà BM = MC
\(\Rightarrow S_{\Delta ACM}=S_{\Delta ABM}=30\left(cm^2\right)\)
Xét \(\Delta ACG\)và \(\Delta MCA\)có chung đường cao hạ từ C xuống đáy AM
Mà \(GA=\frac{2}{3}AM\Rightarrow S_{\Delta AGC}=\frac{2}{3}S_{\Delta AMC}=\frac{2}{3}\times30=20\left(cm^2\right)\)
Lại có \(\Delta CGN\)và \(\Delta AGC\)có chung đường cao hạ từ G xuống AC
Mà \(NC=\frac{1}{2}AC\Rightarrow S_{\Delta CNG}=\frac{1}{2}S_{\Delta AGC}=\frac{1}{2}\times20=10\left(cm^2\right)\)
b) Ta có BM = MC
Mà AM = 2GM
\(\Rightarrow\)G là trọng tâm của tam giác ABC
Lại có BG cắt AC tại N
\(\Rightarrow\)BN là đường trung tuyến tam giác ABC
\(\Rightarrow AN=CN\left(1\right)\)
Mặt khác \(BM=MC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\)MN là đường trung bình của tam giác CAB
\(\Rightarrow MN=\frac{1}{2}AB\)hay \(AB=2MN\)