Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \Delta AMBΔAMB và \Delta DMCΔDMC có:
AB=AC(gt)
AM=MD(gt)
MB=MC(gt)
=>\Delta AMB=\Delta DMC\left(c.c.c\right)ΔAMB=ΔDMC(c.c.c)
b) Vì: \Delta AMB=\Delta DMC\left(cmt\right)ΔAMB=ΔDMC(cmt)
=> \widehat{MAB}=\widehat{MDC}MAB=MDC . Mà hai góc này ở vị trí sole trong
=>AB//DC
# Study well 'v'
a) Xét \(\Delta AMB\) và \(\Delta DMC\) , ta có:
AB = AC (gt)
AM=MD (gt)
MD=MC (gt)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.c.c\right)\)
b) Vì: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB=\widehat{MDC}}\)
\(\Rightarrow AB\) // \(DC\)
#Chúc bạn học tốt ^^

a: Xét ΔAMB và ΔKMC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)
MB=MC
Do đó: ΔAMB=ΔKMC
b: Xét tứ giác BECF có
BE//CF
BE=CF
Do đó: BECF là hình bình hành
Suy ra: BC và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của FE
hay F,M,E thẳng hàng

a)Xét ΔABM và ΔDCM có:
AM=MD
BM=MC
AMB=CMD
=> ΔABM = ΔDCM (c-g-c)
b)Ta có: ΔABM = ΔDCM (cmt)
=> ABM = DCM (2 góc t.ư)
Mà ABM và DCM ở vị trí SLT
=> AB//CD


b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: CD//AB

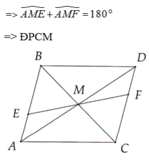

a) CM : tam giác ABM = tam giác DCM
Xét tam giác ABM và tam giác DCM có:
BM = CM ( M là trung điểm của BC )
MA = MD ( gt )
góc BMA = góc CMD ( đối đỉnh )
=> tam giác ABM = tam giác DCM ( c- g - c)
b ) CM AB // CD
Theo chứng minh trên, ta có:
góc BAM = góc CDM ( 2 góc tương ứng của tam giác ABM = tam giác DCM )
mà hai góc này ở vị trí so le trong nên AB // CD
-------
Bạn nên vẽ hình và dùng kí hiệu ra nha, mình ghi nhanh giải cho bạn thôi <3