Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
Xét tam giác AKM và tam giác BKC có:
AK = BK (K là trung điểm của AB)
AKM = BKC ( 2 góc đối đỉnh)
KM = KC (gt)
⇒ Tam giác AKM = Tam giác BKC (c.g.c)
⇒ AM = BC (2 cạnh tương ứng) (1)
AMK = BCK (2 góc tương ứng) mà 2 góc này ở vị trí so le trong
⇒ AM // BC (2)
Xét tam giác AEN và tam giác CEB có:
AE = CE (E là trung điểm của AC)
AEN = CEB (2 góc đối đỉnh)
EN = EB (gt)
⇒ Tam giác AEN = Tam giác CEB (c.g.c)
⇒AN = CB (2 cạnh tương ứng) (3)
ANE = CBE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong
⇒ AN // CB (4)
Từ (1) và (3)
⇒ AM = AN (5)
Từ (2) và (4)
⇒ A, M, N thẳng hàng (6)
Từ (5) và (6)
⇒ A là trung điểm của MN
Vote me~~

C/m tam giác NEA và tam giác BEC có :
AE=EC(gt) NE=EB(gt) NEA = BEC ( hai góc đối đỉnh )
=> tam giác NEA = tam giác BEC ( c.g.c)
=> ANE = CBE ( hai góc tương ứng) => NA // CB (1)
=> NA = CB ( 2 cạnh tương ứng )(3)
Tương tự cm tam giác MKA = tam giác CKB ( c.g.c) => AMK= BCK => AM // CB(2)
=> AM = CB(4)
Từ (1) (2) => N, A, M thẳng hàng (5)
Từ (3) (4) => AN=AM (6)
Từ (5) (6) => A là trung điểm của NM

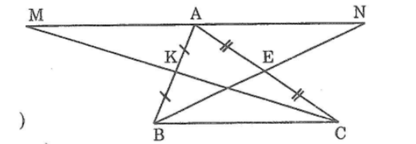
Xét ΔAKM và ΔBKC ta có:
AK = BK (Vì K là trung điểm AB)
∠(AKM) =∠(BKC) (đối đỉnh)
KM=KC (giả thiết)
Suy ra: ΔAKM = ΔBKC(c.g.c)
⇒AM =BC (hai cạnh tương ứng)
Và ∠(AMK) =∠(BCK) (2 góc tương ứng)
Suy ra: AM // BC ( vì có cặp góc so le trong bằng nhau)
Tương tự: ΔAEN= ΔCEB(c.g.c)
⇒ AN = BC (2 cạnh tương ứng)
Và ∠(EAN) =∠(ECB) (2 góc tương ứng)
Suy ra: AN // BC (vì có cặp góc so le trong bằng nhau)
Ta có: AM // BC và AN // BC nên hai đường thẳng AM và AN trùng nhau hay A,M,N thẳng hàng (1)
Lại có: AM = AN ( vì cùng bằng BC) (2)
Từ (1) và (2) suy ra: A là trung điểm của MN

Mình giả bài này rồi nhé, định bào bạn vào TK mình lục nhưng thôi tại mình cung đang rảnh:vv
+Xét \(\Delta AEN\) và \(\Delta CEB:\)
AE=CE(gt)
EN=EB(gt)
\(\widehat{AEN}=\widehat{CEB}\) (2 góc đối đỉnh)
=> \(\Delta AEN=\Delta CEB\left(c-g-c\right)\)
=> AN=CB(2 cạnh t/ứ)(1)
+Xét \(\Delta AKN\) và \(\Delta BKC:\)
AK=BK(gt)
MK=CK(gt)
\(\widehat{AKM}=\widehat{BKC}\) (2 góc đối đỉnh)
=> \(\Delta AKM=\Delta BKC\left(c-g-c\right)\)
=> AM=BC(2 cạnh t/ứ)(2)
Từ (1) và (2) suy ra: AM=AN (3)
Ta có: \(\left\{{}\begin{matrix}\widehat{MAK}=\widehat{CBK}\left(\Delta MAK=\Delta CKB\right)\\\widehat{NAE}=\widehat{BCE}\left(\Delta NAE=\Delta BCE\right)\end{matrix}\right.\)
Mà: \(\widehat{CBK}+\widehat{BAC}+\widehat{BCE}=180^o\)
\(\widehat{MAK}+\widehat{BAC}+\widehat{NAE}=180^o\)
=> M, A, N thẳng hàng (4)
Từ (3) và (4) suy ra: A là trung điểm của MN

Xét tam giác AKM và tam giác BKC có:
AK = BK (K là trung điểm của AB)
AKM = BKC ( 2 góc đối đỉnh)
KM = KC (gt)
=> Tam giác AKM = Tam giác BKC (c.g.c)
=> AM = BC (2 cạnh tương ứng) (1)
AMK = BCK (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => AM // BC (2)
Xét tam giác AEN và tam giác CEB có:
AE = CE (E là trung điểm của AC)
AEN = CEB (2 góc đối đỉnh)
EN = EB (gt)
=> Tam giác AEN = Tam giác CEB (c.g.c)
=> AN = CB (2 cạnh tương ứng) (3)
ANE = CBE (2 góc tương ứng) mà 2 góc này ở vị trí so le trong => AN // CB (4)
Từ (1) và (3)
=> AM = AN (5)
Từ (2) và (4)
=> A, M, N thẳng hàng (6)
Từ (5) và (6)
=> A là trung điểm của MN

Xét tứ giác AMBC có
K là trung điểm của AB
K là trung điểm của MC
Do đó: AMBC là hình bình hành
Suy ra: AM//BC và AM=BC(1)
Xét tứ giác ABCN có
E là trung điểm của AC
E là trung điểm của BN
Do đó: ABCN là hình bình hành
Suy ra: AN//BC và AN=BC(2)
Từ (1) và (2) suy ra A là trung điểm của MN