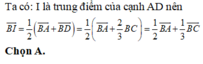Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

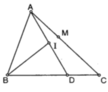
a: Xét ΔAMB có ME là đường phân giác
nên AE/EB=AM/MB=AM/MC(4)
XétΔAMC có MD là đường phân giác
nên AD/DC=AM/MC(5)
Từ (4) và (5) suy ra AE/EB=AD/DC
b: Xét ΔABC có
AE/EB=AD/DC
nên ED//BC
Xét ΔABM có EI//BM
nên EI/BM=AE/AB(1)
Xét ΔACM có ID//MC
nên ID/MC=AD/AC(2)
Xét ΔABC có
ED//BC
nên AE/AB=AD/AC(3)
Từ (1), (2) và (3) suy ra EI/BM=DI/MC
mà BM=CM
nên EI=DI
hay I là trung điểm của ED

\(\Rightarrow\dfrac{OC}{CA}=\dfrac{CI}{CS}\Rightarrow OI\) // \(SA\)
\(OI\subset\left(BID\right)\Rightarrow SA\) // \(\left(BID\right)\)
Nếu thêm phần d là : xác định giao điểm K của BG và (SAC).Tính KB/KG thì làm kiểu gì ạ?

Theo t/c đường tròn, do M là trung điểm BC \(\Rightarrow OM\perp BC\)
Áp dụng định lý Pitago:
\(OM=\sqrt{OC^2-CM^2}=\sqrt{R^2-\left(\dfrac{BC}{2}\right)^2}=3\)
\(\Rightarrow\) Quỹ tích M là đường tròn tâm \(\left(O;3\right)\)
Mặt khác do G là trọng tâm tam giác ABC
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\) G là ảnh của M qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là ảnh của \(\left(O;3\right)\) qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)
\(\Rightarrow\) Quỹ tích G là đường tròn bán kính \(\dfrac{2}{3}.3=2\)

Hôm nay đi cắt lại cái kính, uay đi uay lại mất luôn buổi sáng :(

Bài này để sáng mai thử nghĩ coi sao nhó :) Giờ đi học hóa đã, rảnh inbox tui tán chuyện phiếm xí, dạo này ông anh đi làm đồ án chán chả có ai ngồi nói chuyện cùng :(

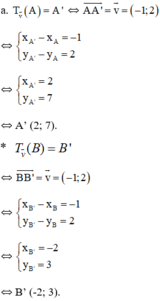
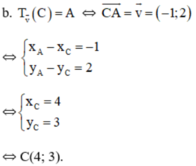
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0