Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
bạn vô đây coi bài nào thích hớp thì xem Cho tam giác ABC. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Gọi H là chân đường vuông góc kể từ B đến AD, K là chân đường vuông góc kẻ từ C đến AE a) Chứng minh rằng HK song song với DE b) Tính HK, biết chu vi tam giác ABC bằng 10 cm Bài 2 Cho tam giác ABC, đường trung tuyến AM. Trên tia đối của tia AM lấy điểm N sao cho AN = AM. Gọi K là giao điểm của CA và NB. Chứng minh NK = 1/2 KB... Xem thêm - Tìm với Google
A B C D E F H
Gợi ý: EF // BC => EF vuông AH
Áp dụng định lí Pitago
\(BE^2=AB^2+BE^2=BD^2+DE^2\)
=> \(\left(BH^2+AH^2\right)+\left(AF^2+FE^2\right)=\left(BH^2+HD^2\right)+\left(EF^2+FD^2\right)\)
=> \(HA^2+AF^2=HD^2+FD^2\)
=> \(\left(AF+FH\right)^2+AF^2=HD^2+\left(HD+FH\right)^2\) ( dùng hằng đẳng thức và rút gọn)
=> \(AF^2+AF.FH=HD^2+HD.FH\)
=> \(\left(AF^2-HD^2\right)+FH\left(AF-HD\right)=0\)
=> AF=HD
a) Vì \(\frac{CD}{AC}=\frac{1,5}{3}=\frac{1}{2}\); \(\frac{CE}{BC}=\frac{2,5}{5}=\frac{1}{2}\)
Nên \(\frac{CD}{AC}=\frac{CE}{BC}=\frac{1}{2}\)
Xét ΔCDE và ΔCAB có
\(\frac{CD}{AC}=\frac{CE}{BC}=\frac{1}{2}\)
Góc DCE=ACB(đối đỉnh)
Vậy hai tam giác đồng dạng với nhau
=> Góc CDE=CAB=90 độ
Vậy ΔCDE là tam giác vuông.
Áp dụng định lí Pi-ta-go vào ΔCDE ta có:
\(CE^2=DC^2+DE^2\Rightarrow DE^2=CE^2-CD^2=2,5^2-1,5^2=4\)
=> \(DE=\sqrt{4}=2cm\).
b) Vì ΔCDE đồng dạng với ΔCAB nên
\(\frac{CD}{AC}=\frac{DE}{AB}\Rightarrow AB=\frac{AC.DE}{CD}=\frac{3.2}{1,5}=4\left(cm\right)\)
ΔABC vuông tại A, đường cao AH, theo hệ thức lượng, ta có:
- \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{4.3}{5}=2,4\left(cm\right)\)
- \(AC^2=CH.BC\Rightarrow CH=\frac{AC^2}{BC}=\frac{3^2}{5}=\frac{9}{5}=1,8\left(cm\right)\)
\(CH=BC-CH=5-1,8=3,2\left(cm\right)\)
GIẢI: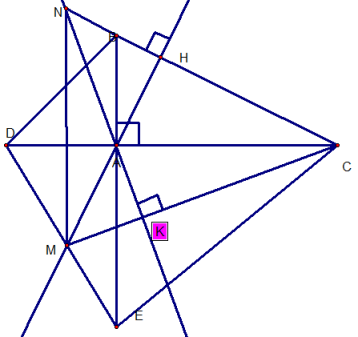
a) Xét Δ ABC và Δ AED, ta có :
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
=> AD 
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : 
=> BD // CE
b) Xét Δ MNC, ta có :
NK
MH
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN
mà : AB
=> MN // AB.
c) Xét Δ AMC, ta có :
=>
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
IM cạnh chung.
mặt khác : 
mà :
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
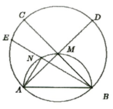
Các tam giác ∆ANE, ∆AMC và ∆BMD vuông cân
=> A E B ^ = A D B ^ = A C B ^ = 45 0
Mà AB cố định nên các điểm A, B, C, D, E cùng thuộc một đường tròn