Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

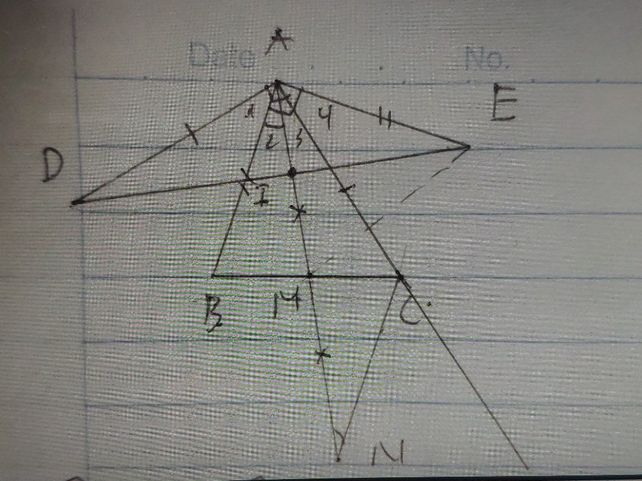
a, Ta có:
góc DAB = góc EAC( Vì cùng phụ góc BAC)
AD= AC
AB=AE
Nên tam giác ABD = tam giác AEC
Vây BD = CEb,
Ta có: ACNB là hình bình hành nên góc ACN + góc BAC = 180độ (1)
Mặt khác ta có : 2( góc DAB +góc BAC) = 2. 90 độ = 180độ
Nên góc DAB + góc EAC + góc BAC + góc BAC = 180 độ
Suy ra DAE + BAC = 180 độ (2)
Từ (1) và (2) ta đc góc DAE = góc ACN
Mà AD = AC; AB= CN nên tam giác ADE = Tam giác cân
c, Ta có: góc NAC = góc ADE ( cmt )
Mà góc NAC + góc DAM = 90 độ nên ADE + góc DAM = 90 độ
Vậy DIA = 90 độ
Áp dụng pytago ta có:\(\frac{AD^2+IE^2}{DI^2+AE^2}=\frac{\left(AD^2+DI^2\right)+\left(AE^2-AI^2\right)}{DI^2+AE^2}=1\)

a)
Ta có góc BAD =góc CAE ( cùng phụ với góc BAC)
Xét tam giác DAB và tam giác CAE có
AD=AC (gt)
góc BAD=CAE (cmt)
AB=AE
=>TAM GIAC BAD= CAE (c-g-c)
=>BD=CE (dpcm)
b)
Xét tam giác ABM và NCM có
MA=MN
góc AMB =NMC (đối đỉnh)
BM =CM (AM là trung tuyến )
=>tam giác ABM=NCM (c-g-c)
=>AB =CN
=>CN=AE
TA có BAM=CNM ( tam giác ABM=NCM)
=>AB //CN
=>BAC+ACN=180 (2 GÓC trong cung phía) (1)
c/m dc DAE+BAC=180 (2)
TỪ (1) và (2)
=>ACN =DAE (CÙNG BÙ BAC)
xét TAM GIÁC ADE và tam giác CAN có
AD=AC (gt)
Góc DAE=ACN
AE=CN
=>Tam giác ADE= CAN (c-g-c)
C) gọi giao điểm của DE và AB là F
Ta có CNM=BAM hay CNM=FAI
MÀ GÓC CNM=AED
=>FAI=AED (=CNM) hay góc FAI=AEF
xét tam giác AFE có FAE=90
= góc AFE +AEF=90
Mà góc FAI=AEF (cmt)
=>góc AFE+FAI =90
=>góc AIF=90
=>\(AI\perp DE\)
XÉT tam giác AEI có AI\(\perp\)DE
=> AE2 =AI2+IE2
=> DI2+AE2=AI2+IE2 +DI2(3)
Xét tam giác ADI CÓ \(AI\perp DE\)
=>AD2=AI2+DI2
=>AD2+IE2=AD2+AI2+DI2 (4)
Từ (3) và(4)
=>AD2+IE2 =DI2+AE2
=>\(\frac{AD^2+IE^2}{DI^2+AE^2}\) =\(1\)(DPCM)