Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự chứng minh được DE =1/2 AC ,EF =1/2 AB và DF =1/2 BC
Do đó: Tam giác ABC đồng dạng với tam giác DEF (c.c.c)
b, Tam giác DEF đồng dạng với tam giác ABC theo tỉ số 2 cạnh tương ứng là DE/AC =2 (hoặc EF/AB,DF/BC thì cũng ra 2)
Chúc bạn học tốt.

Tam giác ABC có:
+) N là trung điểm của AC
+) M là trung điểm của BC
=> MN là ĐTB của tam giác ABC
Tương tự c/m:
+) PN là ĐTB của tam giác ABC+) PM là ĐTB của tam giác ABC
*Có: MN là ĐTB của tam giác ABC
\(\Rightarrow MN=\dfrac{1}{2}AB\)
\(\Rightarrow\dfrac{MN}{AB}=\dfrac{\dfrac{1}{2}AB}{AB}=\dfrac{1}{2}\)
Có: PN là ĐTB của tam giác ABC
\(\Rightarrow PN=\dfrac{1}{2}BC\)
\(\Rightarrow\dfrac{PN}{BC}=\dfrac{\dfrac{1}{2}BC}{BC}=\dfrac{1}{2}\)
Có: PM là ĐTB của tam giác ABC
\(\Rightarrow PM=\dfrac{1}{2}AC\Rightarrow\dfrac{PM}{AC}=\dfrac{\dfrac{1}{2}AC}{AC}=\dfrac{1}{2}\)
Xét tam giác MNP và tam giác ABC có:
\(\dfrac{MN}{AB}=\dfrac{NP}{BC}=\dfrac{MP}{AC}\left(=\dfrac{1}{2}\right)\)

tự kẻ hình ná
trong tam giác AHC có
AK=KH
HN=CN
=> KN là đtb=> KN//AC và KN=AC/2
tương tự, ta có MK//AB và MK=AB/2
MN//BC và MN=BC/2
Xét tam giác ABC và tam giác KMN có
KN/AC=MN/BC=MK/AB(=1/2) (cũng là tỉ số đồng dạng của 2 tam giác)
=> tam giác ABC đồng dạng với tam giác KMN(ccc)

ΔABC~ΔKHG
=>\(\dfrac{AB}{KH}=\dfrac{2}{3}\)
=>\(KH=AB\cdot\dfrac{3}{2}\)
ΔKHG~ΔMNP
=>\(\dfrac{KH}{MN}=\dfrac{1}{3}\)
=>\(\dfrac{AB}{MN}\cdot\dfrac{3}{2}=\dfrac{1}{3}\)
=>\(\dfrac{AB}{MN}=\dfrac{1}{3}:\dfrac{3}{2}=\dfrac{2}{9}\)
=>ΔABC đồng dạng với ΔMNP theo tỉ số \(\dfrac{2}{9}\)

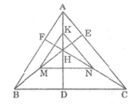
* Trong △ AHB, ta có:
K trung điểm của AH (gt)
M trung điểm của BH (gt)
Suy ra KM là đường trung bình của tam giác AHB.
Suy ra: KM = 1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 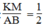 (1)
(1)
* Trong △ AHC, ta có:
K trung điểm của AH (gt)
N trung điếm của CH (gt)
Suy ra KN là đường trung bình của tam giác AHC.
Suy ra: KN =1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 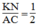 (2)
(2)
* Trong △ BHC, ta có:
M trung điểm của BH (gt)
N trung điểm của CH (gt)
Suy ra MN là đường trung bình của tam giác BHC.
Suy ra: MN = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 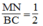 (3)
(3)
Từ (1), (2) và (3) suy ra: 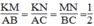
Vậy △ KMN đồng dạng △ ABC (c.c.c)
Ta có: 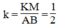

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Ta có: ΔHAC\(\sim\)ΔABC(cmt)
nên \(\dfrac{AH}{AB}=\dfrac{AC}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{AH}{6}=\dfrac{8}{10}=\dfrac{4}{5}\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
a) Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{ACH}\) chung
Do đó: ΔHAC\(\sim\)ΔABC(g-g)