Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

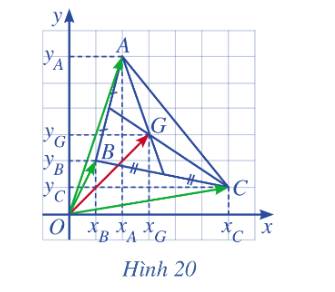
a) Ta có vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \) là: \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
b) Do tọa độ ba điểm A , B và C là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right),C\left( {{x_C},{y_C}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right),\overrightarrow {OC} = \left( {{x_C},{y_C}} \right)\)
Vậy\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Tọa độ điểm G chính là tọa độ của vectơ \(\overrightarrow {OG} \) nên tọa độ G là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

TenAnh1
TenAnh1
A = (-4, -6.26)
A = (-4, -6.26)
A = (-4, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
C = (-4.1, -6.64)
C = (-4.1, -6.64)
C = (-4.1, -6.64)
D = (11.26, -6.64)
D = (11.26, -6.64)
D = (11.26, -6.64)
E = (-4.34, -6.06)
E = (-4.34, -6.06)
E = (-4.34, -6.06)
F = (11.02, -6.06)
F = (11.02, -6.06)
F = (11.02, -6.06)
Có \(BH\perp AC\). (1)
\(\widehat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn) vì vậy\(AC\perp DC\). (2)
Từ (1) và (2) suy ra BH//DC. (3)
Tương tự HC//BD (vì cùng vuông góc với AB). (4)
Từ (3);(4) suy ra tứ giác HCDB là hình bình hành.
b) Do O là trung điểm của AD nên \(\overrightarrow{HA}+\overrightarrow{HD}=2\overrightarrow{HO}\).
Do M là trung điểm của BC nên \(\overrightarrow{HB}+\overrightarrow{HC}=2\overrightarrow{HM}=\overrightarrow{HD}\).
Vì vậy \(\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{HA}+\overrightarrow{HD}=2\overrightarrow{HO}\).
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OH}+\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}\)
\(=3\overrightarrow{HO}+2\overrightarrow{HO}=2\left(\overrightarrow{HO}+\overrightarrow{OH}\right)+\overrightarrow{HO}\)
\(=2.\overrightarrow{0}+\overrightarrow{HO}=\overrightarrow{HO}\).
c) Ta có:
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\)\(=3\overrightarrow{OG}\) (theo tính chất trọng tâm tam giác). (5)
Mặt khác theo câu b)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\). (6)
Theo (5) và (6) ta có: \(\overrightarrow{OH}=3\overrightarrow{OG}\).
Suy ra ba điểm O, H, G thẳng hàng ( đường thẳng Ơ-le).

Tham khảo:
a) Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} + \left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MA} + \overrightarrow {AB} + 2\overrightarrow {AC} = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {AM} = \overrightarrow {AB} + 2\overrightarrow {AC} \\ \Leftrightarrow \overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} \end{array}\)
Trên cạnh AB, AC lấy điểm D, E sao cho \(AD = \frac{1}{4}AB;\;\,AE = \frac{1}{2}AC\)
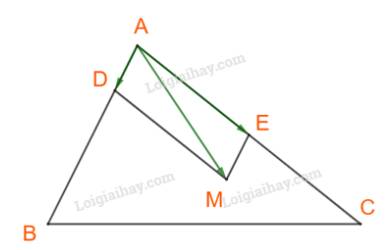
Khi đó \(\overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {AE} \) hay M là đỉnh thứ tư của hình bình hành AEMD.
b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \)
Với mọi điểm O, ta có: \(\left\{ \begin{array}{l}\overrightarrow {OA} = \overrightarrow {OM} + \overrightarrow {MA} ;\;\\\overrightarrow {OB} = \overrightarrow {OM} + \overrightarrow {MB} ;\;\,\\\overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {MC} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + 2\left( {\overrightarrow {OM} + \overrightarrow {MC} } \right)\\ = 4\overrightarrow {OM} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} } \right) = 4\overrightarrow {OM} + \overrightarrow 0 = 4\overrightarrow {OM} .\end{array}\)
Vậy với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \).
Tham khảo cách 2 câu a:
Cách 2:
Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {MC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {MC} + \overrightarrow {CB} } \right) + 2\overrightarrow {MC} = \overrightarrow 0 \)
\(\begin{array}{l} \Leftrightarrow 4\overrightarrow {MC} + \overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow 4.\overrightarrow {CM} = \overrightarrow {CA} + \overrightarrow {CB} \end{array}\)
Gọi D là đỉnh thứ tư của hình bình hành ACBD.
Khi đó: \(\overrightarrow {CD} = \overrightarrow {CA} + \overrightarrow {CB} \)\( \Rightarrow 4.\overrightarrow {CM} = \overrightarrow {CD} \)
\( \Leftrightarrow \overrightarrow {CM} = \frac{1}{4}\overrightarrow {CD} \Leftrightarrow \overrightarrow {CM} = \frac{1}{2}\overrightarrow {CO} \)
Với O là tâm hình bình hành ACBD, cũng là trung điểm đoạn AB.
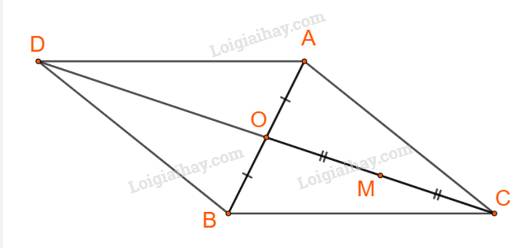
Vậy M là trung điểm của trung tuyến kẻ từ C của tam giác ABC.

câu 2 ( các kí hiệu vecto khi lm bài thỳ b tự viết nhé mk k viết kí hiệu để trả lời cho nhanh hỳ hỳ )
OA+ OB + OC = OA'+ OB' + OC'
<=> OA - OA' + OB - OB' + OC - OC' = 0
<=> A'A + B'B + C'C = 0
<=> 2 ( BA + CB + AC ) = 0
<=> 2 ( CB + BA + AC ) = 0
<=> 2 ( CA + AC ) = 0
<=> 0 = 0 ( luôn đúng )
câu 1 ( các kí hiệu vecto b cx tự viết nhá )
VT = OD + OC = OA + AD + OB + BC = OA + OB + AD + BC = BO + OB + AD + BC = 0 + AD + BC = AD + BC = VP ( đpcm)

A B C P N M
a)
Có: \(3\overrightarrow{OC}-\overrightarrow{OB}=3\left(\overrightarrow{OM}+\overrightarrow{MC}\right)-\left(\overrightarrow{OM}+\overrightarrow{MB}\right)\)
\(=2\overrightarrow{OM}+3\overrightarrow{MC}-\overrightarrow{MB}\)\(=2\overrightarrow{OM}+\overrightarrow{MB}-\overrightarrow{MB}=2\overrightarrow{OM}\). (Đpcm).
b)
Gọi G là trọng tâm tam giác ABC, ta chứng minh G cũng là trọng tâm tam giác MNP.
Ta có: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Ta cần chứng minh: \(\overrightarrow{GN}+\overrightarrow{GM}+\overrightarrow{GP}=\overrightarrow{0}\).
Thật vậy \(\overrightarrow{GN}+\overrightarrow{GM}+\overrightarrow{GP}=\overrightarrow{GC}+\overrightarrow{CN}+\overrightarrow{GB}+\overrightarrow{BM}+\overrightarrow{GA}+\overrightarrow{AP}\)
\(=\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\overrightarrow{CN}+\overrightarrow{BM}+\overrightarrow{AP}\)
\(=\overrightarrow{0}+\overrightarrow{CN}+\overrightarrow{BM}+\overrightarrow{AP}\)
\(=\dfrac{3}{4}\overrightarrow{CA}+\dfrac{3}{4}\overrightarrow{BC}+\dfrac{3}{4}\overrightarrow{AB}\)
\(=\dfrac{3}{4}\left(\overrightarrow{CA}+\overrightarrow{AB}\right)+\dfrac{3}{4}\overrightarrow{BC}\)
\(=\dfrac{3}{4}\overrightarrow{CB}+\dfrac{3}{4}\overrightarrow{BC}=\overrightarrow{0}\).
Vậy G cũng là trọng tâm tam giác MNP. (Đpcm).

\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
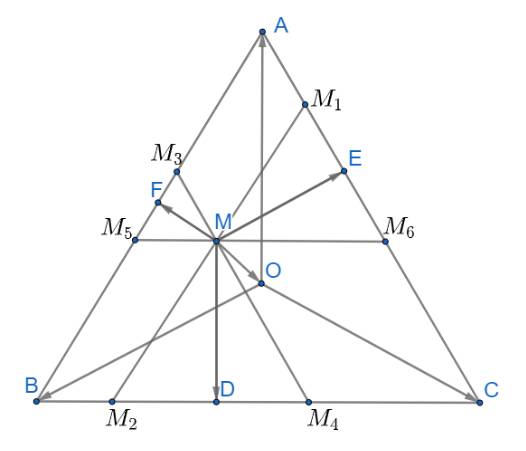
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
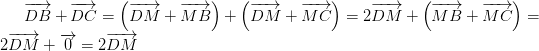
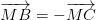
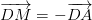
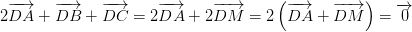
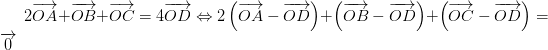
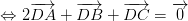 luôn đúng theo câu a
luôn đúng theo câu a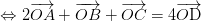 , với O là điểm tùy ý
, với O là điểm tùy ý
Ta có: \(\overrightarrow {OA} = \overrightarrow {OG} + \overrightarrow {GA} \); \(\overrightarrow {OB} = \overrightarrow {OG} + \overrightarrow {GB} \); \(\overrightarrow {OC} = \overrightarrow {OG} + \overrightarrow {GC} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OG} + \overrightarrow {GA} + \overrightarrow {OG} + \overrightarrow {GB} + \overrightarrow {OG} + \overrightarrow {GC} \\ \Leftrightarrow \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {OC} = 3\overrightarrow {OG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)\end{array}\)
Do G là trọng tâm của tam giác ABC nên \(\overrightarrow {GB} + \overrightarrow {GA} + \overrightarrow {GC} = \overrightarrow 0 \)
\(\begin{array}{l} \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {OC} = 3\overrightarrow {OG} + \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {OC} = 3\overrightarrow {OG} \end{array}\)